Kezdőlap


Feladat:	Gy.2478	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Mucsi Zsuzsanna
Füzet:	1988/december, 452 - 454. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Terület, felszín, Hatványközepek közötti egyenlőtlenség, Téglalapok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/április: Gy.2478

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a megadott pont $P$ és rajzoljuk meg a téglalap $B D$ átlóját. Ez két egybevágó derékszögű háromszögre bontja a téglalapot, a kettő közül tekintsük azt, amelyik ‐ esetleg a határán ‐ tartalmazza a $P$ pontot (1. ábra).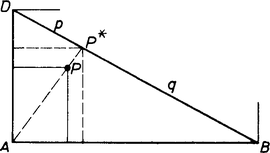

1. ábra

Nagyítsuk úgy az

A

csúcsú résztéglalapot az

A

-ból, hogy

P

rákerüljön a

B D

oldalra. Azt állítjuk, hogy az

A P^{*}

átlójú téglalap területe legfeljebb az

A B D

háromszög területének a fele; ebből következik, hogy a

P

csúcsú résztéglalap területe sem nagyobb

1 / 4

-nél.
Ez az állítás sokféleképpen igazolható. A

P^{*}

-ból induló oldalak két egymáshoz és

A B D

-hez hasonló derékszögű háromszöget vágnak le az

A B D

háromszögből. A

P^{*} D = p, P^{*} B = q

jelöléssel a levágott háromszögek területének összege

\begin{matrix} {(\frac{p}{p + q})}^{2} \cdot t_{A B D} + {(\frac{q}{p + q})}^{2} \cdot t_{A B D} . \end{matrix}

Ez az összeg pedig legalább

\frac{t_{A B D}}{2},

hiszen a négyzetes és a számtani közép közti egyenlőség szerint

\begin{matrix} \sqrt[]{\frac{{(\frac{p}{p + q})}^{2} + {(\frac{q}{p + q})}^{2}}{2}} ≧ \frac{\frac{p}{p + q} + \frac{q}{p + q}}{2} = \frac{1}{2} . \end{matrix}

Könnyen látható, hogy pontosan akkor áll fenn egyenlőség, ha

P = P^{*}

D B

átfogó felezőpontja.

Mucsi Zsuzsanna (Békéscsaba, Sebes Gy. Közg. Szki., II. o. t.)
dolgozata alapján

Megjegyzés. A felhasznált segédtétel következő állítása is igaz: ha egy háromszög a belsejében tartalmaz egy paralelogrammát, akkor a paralelogramma területe nem nagyobb a háromszög területének a felénél.

II. megoldás. A téglalap

O

középpontján átmenő, a téglalap oldalaival párhuzamos egyenesek négy egybevágó téglalapra osztják az

A B C D

téglalapot. Ha a

P

pontot az

A

vagy a

C

csúcsú résztéglalapban vesszük fel, akkor az állítás nyilván igaz, hiszen ekkor valamelyik

P

csúcsú résztéglalapot tartalmazza egy

1 / 4

területű téglalap.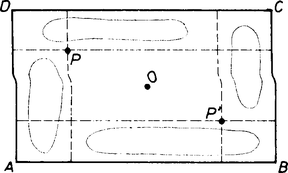

2. ábra

Ha nem ez a helyzet, akkor tekintsük

P

-nek az

O

-ra vonatkozó

P'

tükörképét (2. ábra). A csúcsoknál négy kis egybevágó téglalap keletkezik, és így az

A

és a

C

csúcsú résztéglalapok két-két példánya éppen lefedi azt a "keresztet'', amely úgy jön létre, hogy az

A B C D

téglalapból kivágjuk a vele közös centrumú,

P P'

átlójú téglalapot. Így a két terület kétszeresének összege kisebb, mint az

A B C D

téglalap területe, legalább az egyikük tehát

1 / 4

-nél kisebb területű.

Megjegyzések: 1. Mindkét megoldásból kiderül, hogy a két szóban forgó terület csak úgy lehet

1 / 4

, ha a

P

pontot a téglalap középpontjában vesszük fel.
2. Nem igaz, hogy a két terület között van olyan is, amelyik legalább

1 / 4

; mindkét terület lehet

1 / 4

-nél kisebb. Ez pontosan akkor teljesül, ha a

P

pont a 3. ábrán bevonalkázott tartomány belsejében van. Ezt a tartományt két egybevágó hiperbolaív határolja, melyek a téglalap középpontjában érintik egymást, aszimptotáik a téglalap

A

, ill,

C

csúcsából induló oldalegyenesei, és az oldalakat az

A

, illetve

C

csúcsoktól távolabbi negyedelő pontokban metszik. A feladat állítása egyébként e hiperbolák közvetlen vizsgálatával is igazolható.

3. ábra