Kezdőlap


Feladat:	Gy.2476	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1988/december, 450 - 451. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai bizonyítások, Tengelyes tükrözés, Körülírt kör, Magasságpont, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/március: Gy.2476

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a háromszög $M$ magasságpontjának, ill. az ezen átmenő tetszőleges $e$ egyenesnek a háromszög $B C, A C, A B$ oldalegyeneseire vonatkozó tükörképei rendre $M_{1}, M_{2},$ $M_{3}$ , ill. $e_{1}, e_{2}, e_{3}$ . Ismeretes, hogy az $M_{1}, M_{2},$ $M_{3}$ pontok a háromszög köré írt körön helyezkednek el. A kör és $e$ metszéspontjait $F$ -fel és $G$ -vel, $e_{1} és e_{2}$ metszéspontját pedig $P$ -vel jelöljük (1. ábra); a tükrözések miatt ekkor

\begin{matrix} P M_{1} A ∢ = F M M_{1} ∢ = G M A ∢ = P M_{2} A ∢ . \end{matrix}

1. ábra

A kerületi szögek tétele szerint így

P

a háromszög köré írt körön van, és ugyanez mondható el

e_{1}

és

e_{3}

Q

metszéspontjáról is. Az

e_{1}

egyenesnek és a háromszög köré írt körnek azonban legfeljebb két közös pontja lehet, ezért a

P

Q

M_{1}

pontok közül valamelyik kettő egybeesik. Ha

P \neq M_{1}

és

Q \neq M_{1}

, akkor nyilván

P = Q

, és ez

e_{1}

-nek,

e_{2}

-nek és

e_{3}

-nak is pontja.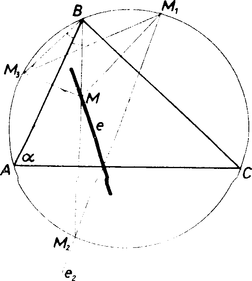

2. ábra

Tegyük fel ezután, hogy pl.

P = M_{1},

azaz

e_{2} = M_{1} M_{2} .

Megmutatjuk, hogy ekkor

e_{3}

is átmegy az

M_{1} = P

ponton, vagyis

e_{3} = M_{3} M_{1} .

Mivel

M_{3}

illeszkedik

e_{3}

-ra, ezért (a 2. ábrán látható elrendezés alapján) elegendő belátni, hogy

e_{3}

ugyanakkora szöget zár be

e_{2}

-vel, mint

M_{3} M_{1}

. Ha

e_{2}

-t

A C

-re tükrözzük, megkapjuk az

e

egyenest, ennek

A B

-re tükrözésével pedig

e_{3}

-hoz jutunk. Az

e_{2}

egyenes tehát

A

körüli

2 α

-szögű forgatással vihető

e_{3}

-ba, így ‐

e_{2} és e_{3}

metszéspontját

R

-rel jelölve ‐

\begin{matrix} M_{3} R M_{2} ∢ = 180^{\circ} - 2 α, \end{matrix}

a kerületi szögek tétele alapján pedig

\begin{matrix} M_{3} M_{1} M_{2} ∢ = M_{3} B M_{2} ∢ = 2 \cdot A B M_{2} ∢ = 2 (90^{\circ} - α) = 180^{\circ} - 2 α . \end{matrix}

Ezzel megmutatjuk, hogy

R = M_{1},

így

e_{3} = M_{3} M_{1}

, következésképpen

M

e_{1}, e_{2}, e_{3}

egyenesek mindegyikére illeszkedik.

Megjegyzés. A megoldás során hallgatólagosan feltételeztük, hogy a háromszög hegyesszögű. Lényegében ugyanígy végezhető el a bizonyítás derékszögű és tompaszögű háromszögre is.