Kezdőlap


Feladat:	Gy.2475	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Keresztély Tibor
Füzet:	1988/december, 448 - 449. oldal		PDF \| MathML
Témakör(ök):	Kombinatorika, Szabályos sokszögek geometriája, Alakzatok köré írt kör, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/március: Gy.2475

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy $m ≦ 4$ . Tudjuk, hogy minden szabályos sokszög körbe írható. Tekintsük az $n$ -szög és az $m$ -szögek köré írható köröket. Az $m$ -szögeknek a $k$ -szög csúcsaitól különböző csúcsai rajta vannak az $n$ -szög köré írt körön, és rajta vannak valamelyik $m$ -szög köré írt körön is. E körök nyilván különbözőek, így legfeljebb két közös pontjuk van. Az $m$ -szögeknek ezért legfeljebb két olyan csúcsuk van, ami a $k$ -szögnek nem csúcsa, azaz $m ≦ 4.$

1. ábra

m = 3

, akkor nyilván

n = k

. Ekkor a

k

-szög középpontja körüli

\frac{360^{\circ}}{k}

szögű elforgatás az alakzatot önmagába viszi, így az szabályos (1. ábra); tehát

k

tetszőleges (2-nél nagyobb egész szám) lehet.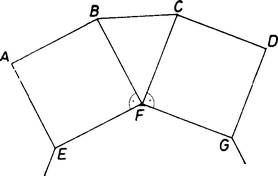

2. ábra

m = 4

esetén legyen

E, F

és

G

k

-szög egymás utáni csúcsa,

A, B, C, D

pedig az

E F

és

F G

oldalak fölé szerkesztett négyzetek további csúcsai (2.ábra). Az

n

-szög csak akkor lehet szabályos, ha

A B = B C = C D

. De

A B = B F

és

C D = C F

, így

B F C

egyenlőoldalú háromszög. Ennek alapján kiszámíthatjuk a

k

-szög egyik szögét:

E F G ∢ = 360^{\circ} - (E F B ∢ + B F C ∢ + C F G ∢) = = 360^{\circ} - (90^{\circ} + 60^{\circ} + 90^{\circ}) = 120^{\circ}

; tehát a

k

-szög csak hatszög lehet. Ha pedig egy szabályos hatszög oldalaira kifelé négyzeteket írunk, akkor a négyzeteknek a hatszög csúcsaitól különböző csúcsai egy olyan tizenkétszöget alkotnak, amelynek minden oldala egyenlő, és minden szöge

150^{\circ}

-os (3. ábra), ezért ez a tizenkétszög valóban szabályos.

3. ábra

k, m, n

számok lehetséges értékei tehát :

m = 3 és n = k

, ahol

k

tetszőleges 2-nél nagyobb szám, vagy

m = 4, k = 6 és n = 12.

Keresztély Tibor (Budapest, Árpád Gimn., I. o. t.)
dolgozata alapján