Kezdőlap


Feladat:	Gy.2458	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Ágoston Kolos , Csirik János
Füzet:	1988/november, 377 - 378. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Terület, felszín, Négyszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1988/január: Gy.2458

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Két esetet kell megkülönböztetnünk, aszerint, hogy az $A B C D$ négyszög konvex vagy konkáv.

1. ábra

Ha az

A B C D

négyszög konvex, akkor a

K L M N

négyszög területét úgy számolhatjuk ki, hogy az

A B C D

négyszög területéből levonjuk az

A L K

D M L

C N M

és

B K N

háromszögek területét (1. ábra). A

B K N

és

B A C

háromszögek hasonlóak, mert megegyezik két-két oldaluk aránya

(B K : B A = B N : B C = 2 : 3)

, az ezen oldalak által bezárt szögük pedig közös. Területük aránya pedig megegyezik a hasonlóság arányának négyzetével, azaz:

\begin{matrix} \frac{T_{B K N}}{T_{B A C}} = \frac{4}{9} . \end{matrix}

(1)

Hasonlóan látható be, hogy

\begin{matrix} \frac{T_{D M L}}{T_{D C A}} = \frac{4}{9} . \end{matrix}

(2)

(1)-ből és (2)-ből viszont ‐ felhasználva, hogy

T_{B A C} + T_{D C A} = T_{A B C D}

‐ következik, hogy

\begin{matrix} T_{B K N} + T_{D M L} = \frac{4}{9} T_{A B C D} . \end{matrix}

(3)

Ugyanígy láthatjuk be, hogy:

\begin{matrix} T_{A L K} + T_{C N M} = \frac{1}{9} T_{A B C D} . \end{matrix}

(4)

Ekkor viszont (3)-at és (4)-et felhasználva:

\begin{matrix} T_{K L M N} = T_{A B C D} - [(T_{B K N} + T_{D M L}) + (T_{A L K} + T_{C N M})] = \\ = T_{A B C D} - [\frac{4}{9} T_{A B C D} + \frac{1}{9} T_{A B C D}] = \frac{4}{9} T_{A B C D} . \end{matrix}

Tehát a keresett arány ebben az esetben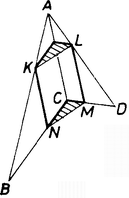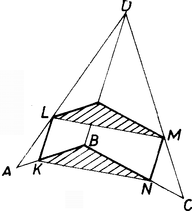

\frac{4}{9}

Ha az

A B C D

négyszög konkáv, akkor a konkáv szögnél levő csúcsból kiinduló átló egyik harmadolópontját felhasználva a

K L M N

négyszöget átdarabolhatjuk egy olyan hatszögbe, amely már teljes egészében az

A B C D

négyszög belsejében fekszik (2. ábra). Ezután ‐ hasonló háromszögeket használva ‐ lényegében az első esettel megegyező módon látható be, hogy a keresett arány most is

\frac{4}{9}

2.a ábra

2.b ábra

Ágoston Kolos (Szeged, Zrínyi I. Ált. Isk., 8. o. t.)
dolgozata alapján

Megjegyzés. Ha a

K

L

M

N

pontok

m : n

arányban osztják az oldalakat, akkor a két négyszög területének aránya

\begin{matrix} \frac{2 m \cdot n}{{(m + n)}^{2}} . \end{matrix}

Csirik János (Szeged, Ságvári E. Gyak. Gimn., II. o. t.)