| Feladat: | Gy.2450 | Korcsoport: 16-17 | Nehézségi fok: könnyű |
| Megoldó(k): | Sztrida Ákos , Tóth Ildikó | ||
| Füzet: | 1988/május, 216 - 217. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Síkgeometriai bizonyítások, Háromszögek egybevágósága, Húrnégyszögek, Érintőnégyszögek, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1987/december: Gy.2450 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Legyen az húrnégyszög átlóinak metszéspontja , a -ből az oldalakra bocsátott merőlegesek talppontjai pedig rendre , , és (1. ábra). Megmutatjuk, hogy a négyszög szemközti szögeinek összege , továbbá hogy e négyszög minden szögfelezője átmegy a ponton. Az előbbiből következik, hogy húrnégyszög, utóbbi pedig azt jelenti, hogy kör írható belé. 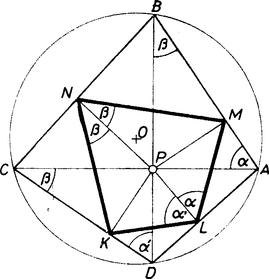 A pontból az oldalakra bocsátott merőlegesek négy húrnégyszögre bontják az eredeti négyszöget, hisz mindegyikükben van két egymással szemközti derékszög. Az húrnégyszögben:
Hasonlóan látható be, hogy ha az egymással egyenlő és szögeket -val jelöljük, akkor , az szög felezője pedig az egyenes. Így a négyszög két szemben levő szögének összege :
Ezzel az állítást beláttuk. Sztrida Ákos (Szekszárd, Garay J. Gimn., II. o. t.) dolgozata alapján Megjegyzések. 1. Az érintőnégyszög legismertebb tulajdonsága az, hogy szemközti oldalainak összege egyenlő. A négyszög érintőnégyszög voltát ennek alapján is be lehet bizonyítani. 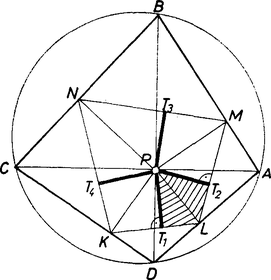 A 2. ábrán a -ből merőlegeseket bocsátunk a négyszög oldalaira. Ekkor az és az derékszögű háromszögek egybevágók, mert átfogójuk közös és az -nél lévő szögük egyenlő. Ezért Hasonlóan látható be, hogy és és így a négyszög szemközti oldalainak összege valóban egyenlő. |