Kezdőlap


Feladat:	Gy.2444	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1988/május, 213 - 214. oldal		PDF \| MathML
Témakör(ök):	Háromszög nevezetes vonalai, Háromszögek hasonlósága, Középpontos tükrözés, Síkgeometriai bizonyítások, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1987/november: Gy.2444

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Tükrözzük a $B$ pontot az $A C$ oldal $F$ felezőpontjára. Legyen a tükörkép $B^{'}$ (1. ábra).

1. ábra

Ekkor a

B^{'} C P

és a

B T P

háromszögek hasonlóak, mert a megfelelő oldalaik párhuzamosak. Így a két háromszög megfelelő oldalainak aránya megegyezik:

\begin{matrix} \frac{C P}{P T} = \frac{B^{'} C}{B T} . \end{matrix}

B^{'} C = A B = A T + T B,

azaz:

\begin{matrix} \frac{C P}{P T} = \frac{A B}{B T} = \frac{A T + T B}{B T} = \frac{A T}{B T} + 1. \end{matrix}

Mivel

C T

A B C

háromszög belső szögfelezője, ezért

\frac{A T}{B T} = \frac{A C}{B C},

és így

\begin{matrix} \frac{C P}{P T} = \frac{A C}{C B} + 1. \end{matrix}

Ezt átrendezve éppen a bizonyítandó állítást kapjuk.

II. megoldás. Jelöljük a háromszög oldalait és szögeit a szokásos módon

a

b

c

, illetve

α

β

γ

-val. Ismert, hogy a

C

-ből induló belső szögfelező hossza:

\begin{matrix} C T = \frac{2 a b}{a + b} cos \frac{γ}{2} . \end{matrix}

(1)

(Az (1) összefüggés mindkét oldalát

\frac{a + b}{2} sin \frac{γ}{2}

-vel szorozva és jobbról balfelé olvasva éppen azt kapjuk, hogy az

A B C

háromszög területe megegyezik az

A T C

és a

B T C

háromszögek területeinek összegével.)

2. ábra

C T

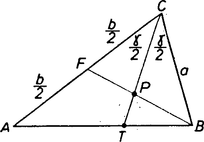egyenes nem csak az

A B C,

hanem az

F B C

háromszögben is szögfelező (2. ábra). Ezért hasonlóan

\begin{matrix} C P = \frac{2 a \cdot \frac{b}{2}}{a + \frac{b}{2}} cos \frac{γ}{2} = \frac{2 a b}{2 a + b} \cdot cos \frac{γ}{2} . \end{matrix}

(2)

(1)-et és (2)-t felhasználva:

\begin{matrix} \frac{C P}{P T} - \frac{A C}{B C} = \frac{C P}{C T - C P} - \frac{A C}{B C} = \frac{\frac{2 a b}{2 a + b} \cdot cos \frac{γ}{2}}{\frac{2 a b}{a + b} \cdot cos \frac{γ}{2} - \frac{2 a b}{2 a + b} \cdot cos \frac{γ}{2}} - \frac{b}{a} . \end{matrix}

Az első törtet

2 a b cos \frac{γ}{2}

-val egyszerűsítve, (ami nem 0) majd rendezve:

\begin{matrix} \frac{C P}{P T} - \frac{A C}{B C} = \frac{\frac{1}{2 a + b}}{\frac{1}{a + b} - \frac{1}{2 a + b}} - \frac{b}{a} = \frac{a + b}{(2 a + b) - (a + b)} - \frac{b}{a} = \frac{a + b}{a} - \frac{b}{a} = 1. \end{matrix}

Ez pedig éppen a bizonyítandó állítás.