Kezdőlap


Feladat:	Gy.2443	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bíró Norbert , Boncz András , Csörnyei Marianna
Füzet:	1988/április, 171 - 172. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Geometriai egyenlőtlenségek, Derékszögű háromszögek geometriája, Súlyvonal, Kör (és részhalmaza), mint mértani hely, Háromszögek szerkesztése, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):	Feladatok: 1987/november: Gy.2443

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Jelöljük a háromszög csúcsait $A, B, C$ vel, súlypontját $S$ -sel, az egymásra merőleges súlyvonalak pedig legyenek $A F$ és $B E$ (1. 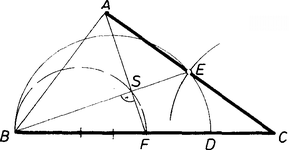ábra).

1. ábra

Mivel a

B

középpontú,

\frac{3}{2}

arányú nagyítás után az

S

pont az

A C

oldal

E

felezőpontjába kerül, ugyanez a nagyítás a

B F

szakasznak a feltétel szerint

S

-en áthaladó Thalesz-körét egy

E

-n áthaladó körbe viszi. Egy újabb

E

-n átmenő vonalat kapunk, ha megrajzoljuk a

C

középpontú,

\frac{A C}{2}

sugarú kört.
A szerkesztés menete ezután a következő. Fölvesszük az ismert

B C

oldalt és megrajzoljuk a

B D

átmérőjű félkört, ahol

D

F

pont képe a

B

középpontú,

\frac{3}{2}

arányú nagyítás során, azaz

B D = 3 B C / 4

. Ebből a körből a

C

középpontú,

\frac{A C}{2}

sugarú kör metszi ki az

A C

oldal

E

felezőpontját. Végül az

A

csúcsot a

C

pont

E

-re vonatkozó tükörképeként kapjuk.
Akkor és csak akkor van megoldás, ha a két kör metszi egymást, ami pontosan akkor igaz, ha az

\frac{A C}{B C}

arány

\frac{1}{2}

és

2

közé esik, azaz

\frac{1}{2} < \frac{A C}{B C} < 2

. Ilyenkor két egybevágó háromszöget kapunk, amelyekre nyilván teljesülnek a feltételek.

II. megoldás. A második ábra jelöléseit használva: a

B S F, A S E

és

B S A

háromszögek derékszögűek, ezért igaz rájuk Pitagorasz tétele.

2. ábra

Az egyes szakaszok hosszának felírásakor felhasználjuk, hogy a súlyvonalak harmadolják egymást:

\begin{matrix} \frac{a^{2}}{4} = 4 x^{2} + y^{2}, \\ \frac{b^{2}}{4} = 4 y^{2} + x^{2}, \\ c^{2} = 4 x^{2} + 4 y^{2} . \end{matrix}

Ezekből egyszerű számolással adódik, hogy

a^{2} + b^{2} = 5 c^{2}

, vagyis

\sqrt[]{5} c = \sqrt[]{a^{2} + b^{2}}

. Az

a

és

b

befogójú derékszögű háromszög átfogója éppen

\sqrt[]{a^{2} + b^{2}}

, tehát ezt a szakaszt meg tudjuk szerkeszteni.

\sqrt[]{5}

éppen az

1

és

2

befogójú derékszögű háromszög átfogója, tehát ha ehhez a háromszöghöz hasonló háromszöget szerkesztünk, melynek átfogója éppen

\sqrt[]{a^{2} + b^{2}} = \sqrt[]{5} c

, akkor a 3. ábrán látható háromszögek hasonlósága miatt:

\frac{c}{1} = \frac{\sqrt[]{5} c}{\sqrt[]{5}},

vagyis a nagyobbik háromszög kisebb befogója

c

3. ábra

Ha pedig a

c

oldalt ilyen módon megszerkesztettük, akkor az eredeti háromszögnek már mindhárom oldalát ismerjük, tehát a háromszöget meg tudjuk szerkeszteni.
A feladatnak akkor van megoldása, ha az

a, b, c

oldalakra teljesül a háromszög-egyenlőtlenség:

\begin{matrix} a + b > c = \sqrt[]{\frac{a^{2} + b^{2}}{5}}; a + c > b; b + c > a . \end{matrix}

Ezek közül az első mindig fennáll, a két utóbbi pedig pontosan akkor, ha

\frac{1}{2} b < a < 2 b

Megjegyzés. A szerkesztés az I. megoldás alapján akkor is elvégezhető, ha a súlyvonalak nem

90^{\circ}

-os, hanem tetszőleges

α

szöget zárnak be, csak

B D

fölé nem Thalesz-kört, hanem a megfelelő látószög körívét kell szerkeszteni.