Feladat: Gy.2441 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Balogh 171 J. ,  Németh László ,  Tóth Péter Zoltán 
Füzet: 1988/április, 168 - 170. oldal  PDF  |  MathML 
Témakör(ök): Kombinációk, Logikai feladatok, Teljes indukció módszere, Gyakorlat
Hivatkozás(ok):Feladatok: 1987/november: Gy.2441

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Balázs kitalálhatja Anna számait egyetlen kérdéssel, ha

B(x,y)=(x+y)(x+y+1)-y=(x+y)2+x
értékét kérdezi meg.
Mivel x és y természetes számok, ezért
(x+y)2≤B(x,y)<(x+y+1)2,(1)
és így Anna számai összegének a négyzete a B(x,y)-nál nem nagyobb négyzetszámok legnagyobbika, azaz
x+y=[B(x,y)].
Anna válasza alapján tehát Balázs először kiszámolhatja a két szám összegét, majd ennek négyzetét B(x,y) -ból kivonva x értékét, végül y-t is.
 

Megjegyzések 1. A feladat szövegezésekor elég szerencsétlen módon kíséreltük meg kizárni, hogy a gondolt számok hatványkitevőként is előforduljanak. Ezt megengedve ugyanis pl. a 2x⋅3y értékéből az egyértelmű prímfelbontás miatt x és y megkapható. A hatványozás korlátozása valójában csupán erre a lehetőségre vonatkozott volna, de a ,,fürdővízzel együtt a gyereket is kiöntöttük'' ‐ emiatt volt szükség az (x+y)2 ,,kerülő úton'' való felírására. Ez nem tartozik a feladat lényegéhez, és emiatt olvasóink elnézését kérjük.
2. A fentieket szem előtt tartva Balázs akkor is boldogulhat egyetlen kérdéssel, ha Anna n darab számra gondolt. Ha ezek a számok x1,x2,...,xn, akkor a
Bn(x1,x2,...,xn)=(x1+...+xn)n+(x1+...+xn-1)n-1+...+(x1+x2)2+x1
formula megfelelő. Fennáll ugyanis ‐ és a binomiális tétel felhasználásával könnyen igazolható ‐ az (1)-hez hasonló
(x1+x2+...+xn)n≤Bn(x1,x2,...,xn)<(x1+...+xn+1)n(2)
egyenlőtlenség, és így a közölt megoldáshoz hasonlóan Balázs rendre kiszámolhatja az
x1+x2+...+xn-1+xn,x1+x2+...+xn-1,⋮x1+x2,x1

mennyiségeket, és így magukat a gondolt számokat is.
3. A teljesség kedvéért megemlítjük, hogy egy z változó n-edik hatványa kifejezhető olyan formulával is, amelyik nem tartalmaz hatványozást. Egy lehetőség például a
zn=((z-1)+1)⋅((z-2)+2)⋅...⋅((z-n)+n)
azonosság kifejtett alakjából nyerhető.
 

II. megoldás. Ahhoz, hogy megoldja a feladatot, Balázs formulájának olyan kétváltozós f(x,y) függvénynek kell lennie, amelyik különböző számpárokhoz különböző egész számokat rendel, tehát kölcsönösen egyértelműen képezi le a természetes számokból készíthető rendezett párok halmazát az egész számok halmazába. Ismeretes, hogy ilyen függvény létezik, ezzel azonban Balázs még nincsen kisegítve, neki ugyanis formulával kell egy ilyen függvényt megadnia, másfelől a függvényérték alapján rá kell találnia a gondolt számpárra, vagyis használnia kell az f függvény inverzét.
Az alábbi táblázat egy ilyen f(x,y) elkészítését szemlélteti.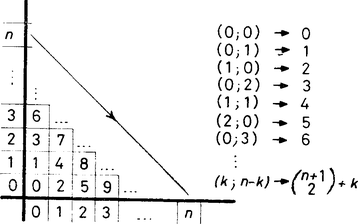
 
 

A táblázat (n+1)-edik átlójában az olyan rendezett számpárokhoz rendelt függvényértékek találhatók, amelyekben az elemek összege n. Azon rendezett számpárok száma, amelyekben az elemek összege kisebb, mint n, éppen (n+12) ‐ ennyiféleképpen választható ki az összeg és a számpár első eleme. Ha ezekhez a számpárokhoz már hozzárendeltük a 0,1,...,(n+12)-1 számokat, akkor a
(0;n),(1;n-1),...,(i;n-i),...,(n;0)
számpárokhoz rendre az
(n+12),(n+12)+1,...,(n+12)+i,...,(n+12)+n=(n+22)-1
számokat rendeljük. Így különböző párokhoz különböző számokat rendelünk, és Balázs megfelelő formulája
(x+y+12)+x.
Ez még tartalmaz 2-vel való osztást, de ennek kétszerese, (x+y+1)(x+y)+2x megfelel a feltételeknek.
A helyettesítési értéket kettővel osztva a táblázat alapján Balázs rátalálhat Anna számaira.
 

Megjegyzések. 4. A fenti megoldásban lényegében azt láttuk be, hogy minden m természetes szám egyértelműen írható
m=(a2)+(b1)
alakban, ahol a>b≥0 ((12)=(01)=0). A megoldásban Balázs az a= =x+y+1,b=x választással használja ezt az eredményt, pontosabban az ehhez a számpárhoz kiszámolt m értékből ,,keresi vissza'' a és b értékét. Ehhez valójában nincs szüksége a táblázatra, hiszen adott m természetes számhoz kell kiszámolnia a nála nem nagyobb (a2) alakú számok legnagyobbikát, hasonlóan ahhoz, ahogyan az első megoldásban m=a2+b értékéből (a=x+y≥x=b) kellett meghatároznia az m-nél nem nagyobb négyzetszámok legnagyobbikát.
5. A második megoldás is általánosítható, igaz ugyanis ‐ és például teljes indukcióval könnyen igazolható ‐, hogy adott n esetén minden m természetes szám egyértelműen írható
m=(ann)+(an-1n-1)+...+(aii)(3)
alakba, ahol an>an-1>...>ai≥i≥1.
Ekkor az
an=x1+x2+...+xn+n,an-1=x1+x2+...+xn-1+n-1,⋮a2=x1+x2+2,a1=x1+1
választással m értékéből az an,an-1,...,a2,a1 számok rendre meghatározhatók, és innen az x1,x2,...,xn értékek is.