Kezdőlap


Feladat:	Gy.2436	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1988/március, 119 - 121. oldal		PDF \| MathML
Témakör(ök):	Síkidomok átdarabolása, Derékszögű háromszögek geometriája, Téglalapok, Négyzetek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1987/október: Gy.2436

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az általánosság megszorítása nélkül föltehető, hogy a szétdarabolandó $A B C$ háromszög rövidebbik befogója, $A C = 1.$ Ekkor a másik befogó, $B C = \sqrt[]{3},$ a háromszög területe pedig $\frac{\sqrt[]{3}}{2},$ ezért a vele egyenlő területű négyzet oldala $\sqrt[]{\frac{\sqrt[]{3}}{2}} .$ Mivel az átdarabolás során a részek területe nem változik, ezért a háromszögből egy $\sqrt[]{\frac{\sqrt[]{3}}{2}}$ oldalú négyzetet kell készítenünk.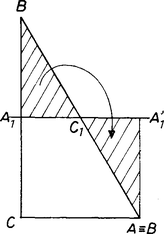

1. ábra

Első lépésben téglalapot készítünk a háromszögből. Vágjuk el az

A_{1} C_{1}

középvonala mentén és forgassuk el a levágott

A_{1} C_{1} B

háromszöget a

C_{1}

körül

180^{\circ}

-kal (1. ábra). Így kapjuk az

A_{1} A'_{1} A C

téglalapot, melynek oldalai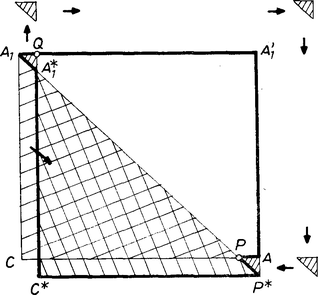

A_{1} A'_{1} = A C = 1

és

A'_{1} A = C A_{1} = \frac{\sqrt[]{3}}{2} .

2. ábra

Legyen a

C A

oldal

C

-től

\sqrt[]{\frac{\sqrt[]{3}}{2}}

távolságra lévő pontja

P

(ilyen pont van, mert

0 < \sqrt[]{\frac{\sqrt[]{3}}{2}} < 1

, az

A_{1} A'_{1}

oldal

A'_{1}

-től ugyanekkora távolságra lévő pontja pedig

Q .

Vágjuk el az

A_{1} A'_{1} A C

téglalapot az

A_{1} P

egyenes mentén, a levágott

A_{1} P C

háromszöget pedig toljuk el az

A_{1} P

egyenessel párhuzamosan úgy, hogy az

A_{1} C

oldal

A_{1}^{*} C^{*}

képének egyenese menjen át a

Q

ponton (2. ábra). Ha a

P

pont képét

P^{*}

-gal jelöljük, akkor

A_{1} Q = P A

miatt az

A'_{1},

A,

P^{*}

pontok is egy egyenesre esnek, ezért az

A_{1} Q A_{1}^{*}

háromszög egybevágó a

P A P^{*}

háromszöggel. Ha most az

A_{1} A'_{1} A P P^{*} C^{*} A_{1}^{*}

idomból levágjuk az

A_{1} Q A_{1}^{*}

háromszöget, és áthelyezzük azt a

P A P^{*}

háromszög helyére, akkor a

Q A'_{1} P^{*} C^{*}

derékszögű négyszöget kapjuk. Ez utóbbi viszont négyzet, mert területe az egyik oldalának a négyzetével egyenlő:

\begin{matrix} A'_{1} Q^{2} = {(\sqrt[]{\frac{\sqrt[]{3}}{2}})}^{2} = \frac{\sqrt[]{3}}{2} . \end{matrix}

Az eljárás során az eredeti háromszöget valóban négy részre vágtuk, mert a három vágás egyike sem metszi át a korábbiakat. A négy rész látható a 3. ábrán. Ezzel a feladatot megoldottuk.

3. ábra

Megjegyzések. 1. A megoldásban leírt módszerrel tetszőleges

a

és

b

oldalú téglalapból

\sqrt[]{a b}

oldalú négyzetet tudunk készíteni. Mivel pedig tetszőleges háromszög könnyen átdarabolható téglalappá, ezért lényegében bebizonyítottuk azt a tételt, hogy egyenlő területű háromszögek véges sok lépésben átdarabolhatók egymásba. Ez speciális esete Bolyai Farkas tételének, mely szerint egyenlő területű sokszögek véges sok lépésben átdarabolhatók egymásba.

4. ábra

2. A 4. ábra azt mutatja be, hogy a feladat csuklós átdarabolással is megoldható, avval az elvvel, amellyel H. Steinhaus, Matematikai Kaleidoszkóp c. munkájában (magyarul: Gondolat, Budapest, 1984, 9‐10. oldal) a szabályos háromszögre oldja meg az itt vizsgált feladatot. Bármelyik

3

pontba teszünk egy-egy csuklót az

F_{1}

F_{2}

F_{3}

F_{4}

pontok közül, ezek együtt tartják a

4

darabot, és a részek

180^{\circ}

-os elforgatásaival az

A B C

háromszög átrendezhető a

P Q R S

négyzetbe.