Kezdőlap


Feladat:	Gy.2412	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Beke T. , Benkő D. , Bodnár B. , Csirik J. , Csordás Z. M. , Csűrös M. , Dienes J. , Hahn Zsuzsanna , Hajnal Z. , Máté Nóra , Peller Z. , Rimaszéki F. , Séra T. , Stoyan R. , Sugár Z. , Veres E.
Füzet:	1988/február, 69 - 72. oldal		PDF \| MathML
Témakör(ök):	Ponthalmazok, Halmazalgebra, Vektorok, Gyakorlat
Hivatkozás(ok):	Feladatok: 1987/április: Gy.2412

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Először is jegyezzük meg, hogy hacsak $P$ és $Q$ nem azonosak $O$ -val, akkor a szerkesztés segédpontjai és így $P \oplus Q$ is egyértelműen létrejönnek. Az $O \equiv P \equiv Q$ esetben legyen $P \oplus Q = O$ .
A második és a harmadik tulajdonság bizonyítása során többször fel fogjuk használni az alábbi könnyen belátható állítást:
(*) Ha $A_{1} B_{1} C_{1}$ és $A_{2} B_{2} C_{2}$ olyan háromszögek a síkon, amelyekre az $A_{1} B_{1}$ és $A_{2} B_{2}$ valamint a $B_{1} C_{1}$ és a $B_{2} C_{2}$ oldalak párhuzamosak, akkor a két háromszög $A_{1} C_{1}$ és $A_{2} C_{2}$ oldalai pontosan akkor párhuzamosak, ha az $A_{1} A_{2}$ , $B_{1} B_{2}$ és $C_{1} C_{2}$ egyenesek egy ponton mennek át, vagy párhuzamosak (1.a, b ábra).

1.a ábra

1.b ábra

Ez az úgynevezett Desargues-féle háromszögtétel egyik speciális esete. Ez utóbbinak bizonyítása megtalálható pl. Reiman István: A geometria és határterületei c. könyvének 341‐342. oldalán.

2. ábra

Először az a) tulajdonságot bizonyítjuk. Vizsgáljuk meg, hogy mik lesznek a feladatban leírt

A

B

C

D

pontok megfelelői, ha

O \oplus P

-t szerkesztjük. Az eljárás szerint

A \equiv O

(2. ábra), ezért

B

x

és

y

egyenesek metszéspontjaként szintén

O

-nak adódik. A

B

-n átmenő

e

-vel párhuzamos egyenes most

e

, és így a

C

e

egyenes és a

P

-n átmenő,

y

-nal párhuzamos egyenes metszéspontja. Így

D \equiv C

, vagyis

O \oplus P = P

. Az a) állítás tehát igaz.

3. ábra

A b) állítás bizonyításához a 3. ábrát fogjuk használni. Ez ugyan a pontoknak csak egy adott elrendezésére vonatkozik, de a további esetek ugyanúgy kezelhetők. Az

A_{1}

B_{1}

C_{1}

D_{1}

pontok jelölik az

A

B

C

D

pontok megfelelőit a

P \oplus Q

szerkesztésénél, míg az

A_{2}

B_{2}

C_{2}

D_{2}

pontok ugyanezek megfelelőit akkor, amikor

Q \oplus P

-t szerkesztjük. Elegendő azt megmutatnunk, hogy a

C_{1} C_{2}

egyenes párhuzamos

x

-szel, mert ez azt jelenti, hogy a

D_{1}

és a

D_{2}

pontok egybeesnek, ebből pedig már következik, hogy a

P \oplus Q

és a

Q \oplus P

pontok azonosak. Az

E

F

G

pontok legyenek rendre a

B_{1} A_{1}

és

C_{1} A_{2}

B_{2} A_{2}

és

C_{2} A_{1}

B_{1} B_{2}

és

C_{1} C_{2}

egyenesek metszéspontjai. Ekkor a

C_{1} B_{1} E

és a

C_{2} B_{2} F

háromszögek megfelelő oldalai párhuzamosak, hiszen a szerkesztés szerint a megfelelő oldalpárok az

e

x

és az

y

egyenesekkel párhuzamosak. Mivel a

C_{1} C_{2}

és a

B_{1} B_{2}

egyenesek a

G

pontban metszik egymást, ezért a (*) állítás szerint az

E F

egyenes is átmegy a

G

ponton.
Tekintsük ezután az

A_{1} E A_{2}

és a

C_{2} G B_{2}

háromszögeket. A csúcsokat az

(A_{1}, C_{2})

(E, G)

(A_{2}, B_{2})

párokba rendezve az összekötő egyenesek átmennek az

F

ponton, ezen kívül az

A_{1} A_{2}

és

C_{2} B_{2}

valamint az

A_{2} E

és

B_{2} G

egyenesek párhuzamosak (előbbiek az

e

-vel, utóbbiak pedig az

y

-nal). A (*) állítás miatt tehát a

G C_{2}

egyenes is párhuzamos az

x

-szel párhuzamos

E A_{1}

egyenessel. Mivel pedig a

G C_{2}

és a

C_{1} C_{2}

egyenesek azonosak, a

C_{1} C_{2}

is a párhuzamos az

x

-szel, mi pedig éppen ezt akartuk bizonyítani.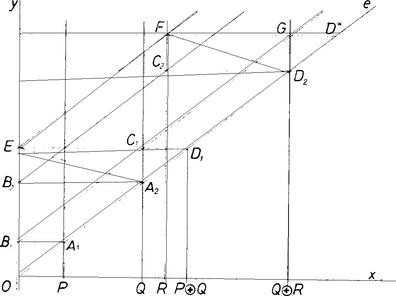

4. ábra

A c) állítás bizonyításához tekintsük a 4. ábrát. Az

A_{1}

B_{1}

C_{1}

D_{1}

pontok most is az

A

B

C

D

pontok megfelelőit jelölik

P \oplus Q

szerkesztésénél, míg az

A_{2}

B_{2}

C_{2}

D_{2}

pontok ugyanezek megfelelőit

Q \oplus R

szerkesztésénél. A további segédpontok megfelelőit az alábbi táblázat tünteti föl.

\begin{matrix} C, Q & Q, R & P \oplus Q, R & P, Q \oplus R \\ A_{1} & A_{2} & D_{1} & A_{1} \\ B_{1} & B_{2} & E & B_{1} \\ C_{1} & C_{2} & F & G \\ D_{1} & D_{2} & D^{*} & D^{*} \\ P \oplus Q & Q \oplus R & (P \oplus Q) \oplus R & P \oplus (Q \oplus R) \end{matrix}

Az előző esethez hasonlóan most is azt kell igazolnunk, hogy a

C

pontnak a

(P \oplus Q) \oplus R

, illetve a

P \oplus (Q \oplus R)

pontok szerkesztésekor kapott megfelelőit, tehát az

F

-et és a

G

-t összekötő egyenes párhuzamos

x

-szel. Ekkor metszi ki ugyanis az

F

-en, illetve a

G

-n átmenő,

x

-szel párhuzamos egyenes ugyanazt a

D^{*}

pontot az

e

egyenesből.
Az

A_{2} B_{2} E

és a

D_{2} C_{2} F

háromszögek csúcsait összekötő egyenesek közül

A_{2} D_{2}

B_{2} C_{2}

és

E F

e

-vel és így egymással is párhuzamosak. Az

A_{2} B_{2}

és

C_{2} D_{2}

, valamint a

B_{2} E

és

C_{2} F

oldalak párhuzamosak az

x

, illetve az

y

egyenessel, ezért a (*) állítás miatt a háromszögek harmadik,

A_{2} E

és

D_{2} F

oldalai is párhuzamosak. Ekkor viszont az

A_{2} C_{1} E

és a

D_{2} G F

háromszögekben ‐ ahol az

A_{2} D_{2}

C_{1} G

E F

egyenesek párhuzamosak ‐ az

A_{2} E

és a

D_{2} F

oldalak mellett az

A_{2} C_{1}

és a

D_{2} G

oldalak is párhuzamosak, tehát a (*) állítás miatt a két háromszögben a harmadik oldalak,

E C_{1}

és

F G

is azok. Mivel

E C_{1}

párhuzamos

x

-szel, ezért

F G

is az, és ezt akartuk bizonyítani. A c) tulajdonság tehát szintén teljesül.
Ezzel a bizonyítást befejeztük.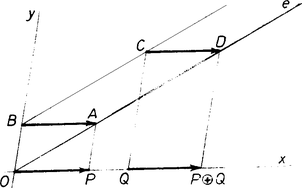

II. megoldás. A szerkesztési eljárás szerint az alábbi vektorok megegyeznek (5. ábra):

5. ábra

\begin{matrix} \vec{O P} = \vec{B A} = \vec{C D} = \vec{Q (P \oplus Q)} . \end{matrix}

Ha most az

O

pontból helyvektorokat indítunk a megadott pontokhoz, akkor a fentiek szerint

\begin{matrix} \vec{O P} + \vec{O Q} = \vec{O Q} + \vec{Q (P \oplus Q)} = \vec{O (P \oplus Q)} . \end{matrix}

Ez azt jelenti, hogy a

\oplus

művelet az

x

egyenesen megegyezik a vektorok összeadásával. A vektorok összeadása viszont rendelkezik az a), b), c) tulajdonságokkal, tehát azokkal a

\oplus

művelet is rendelkezik.
Ezzel az állítást beláttuk.

Megjegyzések: 1. Az I. megoldás látszólag sokkal bonyolultabb, mint a II. Ez azért van, mert az I. megoldásban csak Desargues tételét használjuk fel, míg a II. megoldásban a vektorok műveleti tulajdonságait. Ezeknek a műveleti tulajdonságoknak a precíz bizonyítása legalább olyan hosszadalmas, mint az I. megoldás.
2. Ha

x

és

y

egy derékszögű koordináta-rendszer két tengelye,

e

pedig az

y = x

egyenletű egyenes, akkor a

\oplus

művelet megegyezik a valós számok megszokott összeadásával.