Feladat: Gy.2410 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Ambrus Beáta ,  Balogh 171 J. ,  Barabás 479 Gy. ,  Benczúr P. ,  Boda Z. ,  Csirik J. ,  Hajnal Z. ,  Hídvégi Z. ,  Jónás A. ,  Király Rita ,  Kondacs A. ,  Kőrösi A. ,  Kozma K. ,  Lois L. ,  Máté Nóra ,  Péter I. ,  Pór A. ,  Sándor B. ,  Semsey Sz. ,  Siklér F. ,  Somfai Ellák ,  Sustik M. ,  Szabó 713 D. ,  Szakács Á. ,  Szamuely T. ,  Szilágyi B. ,  Temesvári A. ,  Tornyi L. 
Füzet: 1988/január, 18 - 20. oldal  PDF  |  MathML 
Témakör(ök): Súlypont, Kombinatorikai leszámolási problémák, Oszthatóság, Négyzetrács geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1987/április: Gy.2410

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a síkbeli négyzetrács rácspontjait egy derékszögű koordináta-rendszer egész koordinátájú pontjainak. Ismeretes, hogy az A1(x1,y1), A2(x2,y2), A3(x3,y3) csúcsú háromszög súlypontjának koordinátái:

xs=x1+x2+x33ésys=y1+y2+y33.
Egy háromszög súlypontja tehát pontosan akkor rácspont, ha a csúcsok első, illetve második koordinátáinak az összege osztható 3-mal. Hívjunk három rácspontot "jónak'', ha ez fennáll rájuk.
Megmutatjuk, hogy a feladatban kimondott állítás a 8-nál nagyobb természetes számokra igaz. Ehhez nyilván elegendő egyrészt 9 pontra igazolni az állítást, másrészt mutatni 8 olyan rácspontot, amelyre az állítás nem teljesül.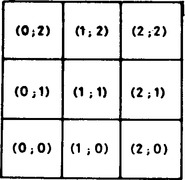
 
 
1. ábra
 

Az egyes koordináták háromféle maradékot adhatnak 3-mal osztva, így összesen 3⋅3=9 típusú rácspont lehetséges. Ezeket a lehetőségeket tartalmazza az 1. ábra táblázata.
Tekintsünk most 9 rácspontot, és helyezzük el őket az 1. ábra celláiban aszerint, hogy a koordinátáik milyen maradékot adnak 3-mal osztva. Ha van olyan cella, ahová legalább három pont kerül, akkor nyilván készen vagyunk, hiszen három egyenlő maradék összege osztható 3-mal.
Ha sehol sincs kettőnél több, akkor legalább 5 cellába kerül rácspont, hisz a pontok száma 9. Válasszunk ki öt ilyen "foglalt'' cellát, illetve mindegyikükben egy-egy rácspontot. Azt állítjuk, hogy ezek között van három jó.
Nyilván bármely két különböző cellához van egy és csak egy olyan harmadik, hogy az e három cellába kerülő három rácspont jó, így összesen (92)/3=12 olyan jó hármas van, ahol különböző cellákból valók az elemek.
Tekintsük ezután az 5 kiválasztott rácspont által meghatározott (52)=10 jó hármast. Ha belátjuk, hogy ezek a hármasok nem lehetnek valamennyien különbözők, akkor készen vagyunk, ugyanis két különböző pontpár éppen akkor határozza meg ugyanazt a jó hármast, ha az éppen a két pár pontjainak az egyesítése, és így mindhárom pontja szerepel a megadott pontok között.
Osszuk ehhez az összesen 12 jó hármast négy, egyenként három elemű csoportra a 2. ábra szerint. (Az egyes csoportokban az azonos jelű pontok alkotják a jó hármasokat.)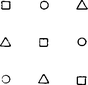
 
 
2.a) ábra
 

 
 
2.b) ábra
 

 
 
2.c) ábra
 

 
 
2.d) ábra
 

Ha az 5 pont által meghatározott 10 jó hármas között nincsenek azonosak, akkor a 2. ábra négy csoportja közül legalább egynek mindhárom eleme ott van a fenti 10 jó hármas között. Az egyes csoportokon belül viszont semelyik két hármasnak nincs közös pontja, vagyis egy csoport három hármasának meghatározásához 6 pontra van szükség! Mivel nekünk csak öt pontunk van, a 10 hármas között valóban kell, hogy legyenek azonosak, amiből a fentiek szerint következik, hogy a feladat állítása 9 pont esetén igaz.
Egy nyolcelemű ellenpélda a következő :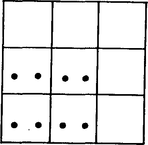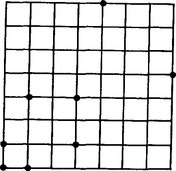
(0;0),(0;0),(0;1),(0;1),(1;0),(1;0),(1;1),(1;1).
Összesen négy cellába kerülnek pontok, mindegyikbe kettő-kettő (3/a ábra), és a fentiek szerint nyilván nincs köztük három jó. A 3/b ábrán nyolc olyan rácspont látható, amelyek közül semelyik három nem esik egy egyenesre, koordinátáik pedig éppen az adott celláknak megfelelő maradékot adják.
 
 
3.a) ábra
 

 
 
3.b) ábra
 

Megjegyzések. 1. A feladatban nem volt lényeges az a megszorítás, hogy a megadott pontok közül semelyik három ne essék egy egyenesre, amennyiben elfajuló háromszög súlypontját is a csúcsok koordinátái számtani közepeként értelmezzük.
2. A feladat annak az ismert állításnak a "kétdimenziós'' általánosítása, mely szerint öt egész szám között mindig van három, amelyek összege 3-mal osztható. Tulajdonképpen azt láttuk be, hogy kilenc, egész számokból álló számpár között mindig van három olyan, ahol mind az első, mind pedig a második elemek összege osztható 3-mal. A feladat nyilván tovább általánosítható. Másfelől maga az "egydimenziós'' állítás is csak speciális esete az alábbi tételnek : ha adott 2n-1 darab egész szám, akkor mindig kiválasztható közülük pontosan n, amelyek összege n-nel osztható. Ennek bizonyítása megtalálható például Csirmaz László: Kedvenc problémáim c. rovatában a KÖMAL 1982/10 számának 193‐195. oldalán.