Kezdőlap


Feladat:	Gy.2405	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Balogh J. , Barasbás Gy. , Benkő D. , Bíró 100 A. , Bodnár Z. , Botrágyi T. , Eiben P. , Fazekas Anna , Fleiner T. , Héray A. , Hídvégi Z. , Hugyecz T. , Károlyi A. , Kozma K. , Lois L. , Máté Cs. , Pásztor 625 G. , Peták A. , Pór A. , Pór Attila , Siklér F. , Sustik M. , Szabó 440 Á. , Szamuely T.
Füzet:	1987/november, 392 - 394. oldal		PDF \| MathML
Témakör(ök):	Egészrész, törtrész függvények, Gúlák, Kombinatorikus geometria térben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1987/március: Gy.2405

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A metszetsokszög csúcsait nyilván a metsző síknak és a gúla éleinek a metszéspontjaiként kapjuk. Jelölje $S$ a gúla alaplapjának a síkját, $T$ pedig a metsző síkot. Ha $S$ és $T$ párhuzamos, akkor $T$ csak a gúla $A$ csúcsából induló $n - 1$ élt metszheti, az ilyen metszetsokszögnek tehát legfeljebb $n - 1$ oldala lehet.
Ha $S$ és $T$ metszik egymást, akkor jelölje $e$ a közös egyenesüket. Osszuk a gúla $S$ -re illeszkedő $n - 1$ csúcsát három csoportba aszerint, hogy az $e$ egyenes melyik partján helyezkednek el. Jelölje $k_{1}$ az $e$ -re illeszkedő, $k_{2}$ és $k_{3}$ pedig a két különböző félsíkban lévő csúcsok számát. Ekkor nyilván $k_{1} + k_{2} + k_{3} = n - 1$ .
A metszetsokszög csúcsait a $T$ síknak a gúla alapjának kerületével, illetve az $n - 1$ darab oldaléllel való metszéspontjaiként kapjuk. Külön-külön adunk becslést az egyes típusú metszéspontok számára.
A $T$ sík, azaz az $e$ egyenes úgy metszheti a gúla alaplapjának kerületét, ha egy megfelelő oldal az $e$ különböző partjára eső csúcsokat köt össze, vagy pedig valamelyik végpontja az $e$ -re illeszkedik. Mivel pedig az $e$ által meghatározott két félsík bármelyikéből legfeljebb annyi él léphet ki, mint az ide eső csúcsok számának a kétszerese, ezért $T$ az alaplap kerületét legfeljebb $k_{1} + 2 \cdot {min}_{}^{} (k_{2}, k_{3})$ pontban metszheti. (min ( $x, y$ ) az $x$ és $y$ valós számok közül a nem nagyobbikat, max ( $x, y$ ) pedig a nem kisebbiket jelöli.) Ez meg is valósítható, amennyiben a kevesebb/nem több csúcsot tartalmazó félsík nem tartalmaz teljes oldalt, azaz minden itteni csúcs az $e$ másik partjára eső csúccsal van összekötve (1. ábra).

1. ábra

A gúlának az

S

-re nem illeszkedő

A

csúcsából induló

n - 1

darab oldalélét a

T

sík az alaplapon létrejövő metszéspontok számától függetlenül 1,

k_{2}

vagy pedig

k_{3}

pontban metszheti aszerint, hogy az

A

csúcs hogyan helyezkedik el a metsző síkhoz képest: illeszkedik rá, vagy pedig a

T

sík elválasztja a

k_{2}

, illetve a

k_{3}

elemű ponthalmaztól.
A

T

sík tehát legfeljebb

k_{1} + 2 \cdot {min}_{}^{} (k_{2}, k_{3}) + {max}_{}^{} (1, k_{2}, k_{3}) = k_{1} + k_{2} + k_{3} + {min}_{}^{} (k_{2}, k_{3}) = n - 1 + {min}_{}^{} (k_{2}, k_{3})

pontban metszheti a gúla éleit, hiszen

{min}_{}^{} (k_{2}, k_{3}) + {max}_{}^{} (1, k_{2}, k_{3}) = k_{2} + k_{3}

. Mivel

{min}_{}^{} (k_{2}, k_{3}) ≦ \frac{k_{2} + k_{3}}{2} ≦ [\frac{n - 1}{2}]

, ezért a metszetsokszögnek legfeljebb

n - 1 + [\frac{n - 1}{2}]

csúcsa lehet.
Könnyű belátni, hogy ez a maximum minden szóba jövő, azaz 3-nál nagyobb

n

érték mellett elérhető, tehát ha

n ≧ 4

, akkor van olyan

n

-csúcsú gúla, amelyet egy alkalmas

T

sík éppen egy

n - 1 + [\frac{n - 1}{2}]

csúcsú sokszögben metsz.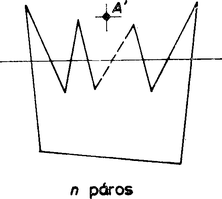

2.a ábra

2.b ábra

Tekintsünk ugyanis a gúla alaplapjaként egy

n - 1

oldalú sokszöget és egy azt metsző

e

egyenest az

n

paritásától függően a 2.a), illetve a 2.b) ábra szerint. Itt

k_{1} = 0

, és ha

n

páratlan, akkor

k_{2} = k_{3} = \frac{n - 1}{2}

, ha pedig

n

páros, akkor

k_{2} = [\frac{n - 1}{2}]

és

k_{3} = [\frac{n}{2}]

. Az alaplapon így mindkét esetben

2 k_{2}

metszéspont keletkezik.
Ha például

T

merőleges az alaplap síkjára, és a gúla

n

-edik csúcsa abban a féltérben van, amelyik nem több, illetve kevesebb csúcsát tartalmazza az alaplapnak, akkor az oldaléleken

k_{3}

metszéspont jön létre. (A 2. ábrákon

A'

jelöli az

A

csúcs merőleges vetületét az alaplapon.)
A metszetsokszög oldalainak a száma így

2 k_{2} + k_{3}

, ami páratlan

n

-re

2 \frac{n - 1}{2} + \frac{n - 1}{2} = (n - 1) + [\frac{n - 1}{2}]

, páros

n

-re pedig

[\frac{n - 1}{2}] + ([\frac{n - 1}{2}] + \frac{n}{2}) = [\frac{n - 1}{2}] + (n - 1)

, tehát a kapott maximum valóban elérhető.

Megjegyzések. 1. Bizonyos esetekben a metszetsokszög nem összefüggő, ez azonban nem befolyásolja a csúcsok, illetve élek maximális számára tett megállapításunkat.
2. Ha a gúla konvex, akkor a metsző sík minden lapot legfeljebb egyszer metszhet, tehát a metszetsokszög legfeljebb

n

oldalú. Ez be is következik, ha

T

A

csúcsból induló

n - 1

él közül pontosan egyet nem metsz, ekkor ugyanis két szomszédos alapélen keletkezik metszéspont. Az

n = 5

esetben ez látható a 3. ábrán.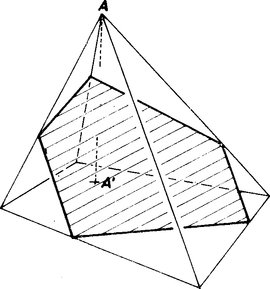

3. ábra

A megoldással próbálkozók nagyobb része csak ezzel az egyszerűbb esettel foglalkozott.