Feladat: Gy.2404 Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1987/december, 449 - 451. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek egybevágósága, Pont körüli forgatás, Trigonometriai azonosságok, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Húrnégyszögek, Gyakorlat
Hivatkozás(ok):Feladatok: 1987/március: Gy.2404

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen N az AM szakasz azon pontja, melyre BM=AN (1. ábra). Ekkor a BMF és az ANF háromszögek egybevágóak, mert megegyezik két-két oldaluk (BF=AF és BM=AN) valamint az általuk bezárt szög (FAN∢=FBM∢, mert mindkettő az MF⌢ ívhez tartozó kerületi szög). Tehát FM=FN , az FNM háromszög egyenlő szárú, ezért az F-ből induló magasság T talppontja felezi az NM szakaszt.

 
 
1. ábra
 

Ezek után a bizonyítandó állítás már könnyen adódik:
AT=AN+NT=BM+MT.

 

Megjegyzés. A feladatra sokféle megoldás adható, az alábbiakban öt további lehetőséget vázolunk, végiggondolásukat az olvasóra hagyva.
I. vázlat. Forgassuk el a BM húrt a kör középpontja körül pozitív irányba úgy, hogy a B pont az F-be kerüljön (2. ábra), és legyen eközben az M pont képe M'. Ekkor az M'F és az AM húrok párhuzamosak (MF⌢=M'A⌢), ahonnan a szimmetria miatti egyenlőségek fölhasználásával a bizonyítandó állítást kapjuk.
 
 
2. ábra
 

II. vázlat. Ha L jelöli az FT és a kör második metszéspontját és LB a B'-ben metszi AM-et (3. ábra), akkor az L-nél létrejövő egyíves szögek egyenlősége miatt ALB' egyenlő száru háromszög. Könnyen látható,hogy az A, illetve a B csúcsú kétíves szögek is egyenlők (ALBM húrnégyszög), és ezután AT=TB' és MB=MB' felhasználásával adódik az állítás.
 
 
3. ábra
 

III. vázlat. "Hajtsuk ki'' az AMB^ töröttvonalat az AB' szakasszá a 4. ábra szerint. Ekkor AF=B'F-et kell igazolnunk, hisz T ekkor felezi AB'-t.
 
 
4. ábra
 

Thalész tétele szerint az FM-re M-ben állított merőleges a BA⌢ ív F* felezőpontjában metszi a kört, és így felezi az AMB szöget. Az FM így ennek külső szögét, a BMB' szöget felezi, tehát BM=B'M miatt BF=B'F, azaz AF=BF miatt valóban  AF=B'F.
IV. vázlat. Az F pontból a BM egyenesre bocsátott merőleges talppontját P -vel jelölve könnyen kapjuk, hogy egybevágók az ATF és a BPF, illetve  az FTM és az FPM derékszögű háromszögek (5. ábra), ahonnan a bizonyítandó állítás már következik.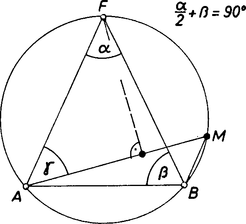
 
 
5. ábra
 

 
 
6. ábra
 

V. vázlat. Feltéve, hogy a kör sugara egységnyi, a 6. ábrán látható α, β, γ szögek felhasználásával kapjuk, hogy AT=2cosα2cosγ, TM=2sinγsinα2 és BM=2sin(α+β+γ). Innen egyszerű számolással adódik a bizonyítandó állítás.