Kezdőlap


Feladat:	Gy.2397	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1987/október, 312 - 313. oldal		PDF \| MathML
Témakör(ök):	Kocka, Terület, felszín, Paralelogrammák, Szélsőérték-feladatok differenciálszámítás nélkül, Gyakorlat
Hivatkozás(ok):	Feladatok: 1987/február: Gy.2397

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a szóban forgó testátló két végpontja $A$ , illetve $G$ . Ez a két pont rajta van a metsző síkok bármelyikén épp úgy, mint a kocka minden egyes lapjának a kerületén. Így az $M$ metszetsokszög minden oldala valamelyik végpontjaként tartalmazza az $A$ vagy pedig a $G$ csúcsot, ami csak úgy lehetséges, ha $M$ négyszög, melynek $A$ és $G$ átellenes csúcsai. (Mivel a kocka és a metsző sík együttese középpontosan szimmetrikus, ezért $M$ valójában paralelogramma.) Jelölje $P$ és $Q$ az $M$ másik két átellenes csúcsát.

1. ábra

Tekintsük a kocka éleinek és az

M

-nek a vetületét egy, az

A G

-re merőleges síkon (1. ábra). Mint ismeretes, az élhálózat vetülete egy

\sqrt[]{6} / 3

oldalú szabályos hatszög és annak három főátlója. Az

M

vetülete ekkor egy, a fenti hatszög középpontján átmenő

P' Q'

szakasz, a négyszög

P Q

átlójának a vetülete.

2. ábra

A merőleges vetítés miatt

P' A

és

Q' A

A P G

, illetve a

G Q A

háromszögekben a közös

A G

oldalhoz tartozó magassággal egyenlők (2. ábra), ezért az

M

négyszög területe,

t = \frac{1}{2} P' Q' \cdot A G

.
Ebben a szorzatban

A G

állandó, így

t

akkor a legkisebb, illetve a legnagyobb, ha a

P' Q'

vetületszakasz a legkisebb, illetve a legnagyobb. A metsző sík forgása közben a

P' Q'

a hatszög középpontja körül forog és nyilván minden lehetséges helyzetet fölvesz. Akkor lesz a legrövidebb, ha merőleges a hatszög két szemközti oldalára, és akkor a leghosszabb, ha a hatszög valamelyik főátlójával esik egybe. Ez a két helyzet a 3.a és 3.b ábrán látható metszeteknek felel meg. Az első esetben

P

és

Q

élfelező pontok, hiszen vetületeik is azok a hatszög kerületén. Ilyenkor

P' Q'

a kocka lapátlójával,

\sqrt[]{2}

-vel egyenlő, így

t = \frac{\sqrt[]{6}}{2}

. A második esetben

P

és

Q

átellenes kockacsúcsok,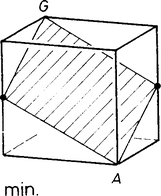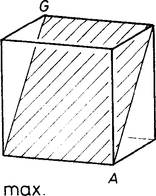

P' Q' = \frac{2 \sqrt[]{6}}{3}

, így

t = \sqrt[]{2}

3.a ábra

3.b ábra

A metszet területe tehát a

\frac{\sqrt[]{6}}{2} \approx 1,225

és a

\sqrt[]{2} \approx 1,414

határok között változik, mindkét szélsőértéket fölveszi, és mivel

M

területe a két szélsőérték között nyilván folytonosan változik, ezért minden közbülső értéket is fölvesz.