| Feladat: | Gy.2380 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Pásztor Gábor | ||
| Füzet: | 1987/november, 388 - 389. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Beírt háromszög, Háromszögek nevezetes tételei, Indirekt bizonyítási mód, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1986/december: Gy.2380 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megmutatjuk, hogy nem léteznek a feltételeknek eleget tevő háromszögek. A megoldás során többször fel fogjuk használni a következő ‐ nyilvánvaló ‐ lemmát: 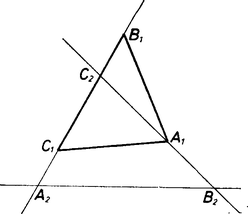 A csúcsai tehát csak úgy helyezkedhetnek el a oldalegyenesein, hogy ezek egyikén két csúcs van, egy másikon egy, a harmadikon pedig egy sem. Feltehető tehát, hogy a két háromszög, és az 1. ábrán látható módon helyezkedik el. A lemma szerint ekkor a háromszög és oldalegyenesei a háromszög egyetlen csúcsát sem tartalmazzák, és így mindhárom csúcsának a egyenesen kell lennie. Ez nyilván nem lehet, így kiinduló feltevésünk hamis volt, páronként egymásba írt két háromszög tehát valóban nem létezik. Megjegyzések: 1. A Gy. 2341. megoldása során (KöMaL 36. évfolyam 10. szám 448. old.) láttuk, hogy a térben már létezik két, páronként egymásba írt tetraéder. 2. Három darab háromszög már megadható úgy, hogy az első a másodikba, a második a harmadikba, a harmadik pedig az elsőbe van írva (2.ábra). 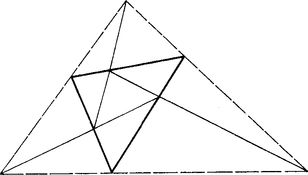 |