Kezdőlap


Feladat:	Gy.2373	Korcsoport: 18-	Nehézségi fok: átlagos
Megoldó(k):	Antos A. , Bajusz Orsolya , Beke T. , Bíró 100 A. , Csirik J. , Dienes J. , Fejérdy Zsófia , Fleiner T. , Károlyi A. , Kecskés K. , Keleti T. , Kondacs A. , Kosztolnyik T. , Mohácsi P. , Pásztor Gabriella , Peták A. , Petri Z. , Sándor B. , Sikér F. , Sugár Z. , Sustik M. , Szabó 713 D. , Tornyi L. , Tóth 178 G. , Vörös T. , Wiandt T. , Wolkensdorfer P.
Füzet:	1987/november, 386 - 388. oldal		PDF \| MathML
Témakör(ök):	Térelemek és részeik, Térgeometriai bizonyítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1986/november: Gy.2373

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Először a következő állítást bizonyítjuk be:

(

*

) Ha a térben három nem egy síkban lévő egyenes páronként egysíkú, akkor az egyenesek vagy egy pontban találkoznak, vagy pedig párhuzamosak.
Ezután megmutatjuk, hogy a

P_{11} P_{22}

P_{13} P_{32}

P_{23} P_{31}

, egyenesek nincsenek egy síkban, de páronként egysíkúak, amiből feladatunk állítása következik.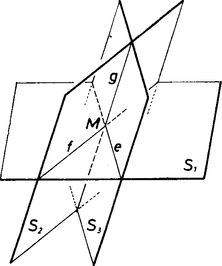

1. ábra

Legyenek tehát

e

f

és

g

a (

*

) állításban szereplő egyenesek. Legyen az

e

és

f

egyenesek síkja

S_{1}

f

és

g

síkja

S_{2}

g

és

e

síkja pedig

S_{3}

. Tegyük fel, hogy az

e

és

f

egyenesek metszik egymást és jelölje a metszéspontot

M

(1. ábra). Ekkor

M

benne van az

S_{3}

síkban, mert rajta van az

e

egyenesen, és benne van az

S_{2}

síkban is, mert rajta van az

f

egyenesen. Az

M

pont tehát rajta van az

S_{2}

és

S_{3}

síkok egyértelműen létező metszésvonalán (itt használjuk ki, hogy

S_{1}

S_{2}

, és

S_{3}

különböző síkok), a

g

egyenesen. A három egyenes tehát valóban egy ponton halad át. Ha tehát egyeneseink között vannak metszők, akkor ezek metszéspontján a harmadik is átmegy. Ezért ha az

e

és

f

egyenesek párhuzamosak (a feltétel miatt kitérők nem lehetnek), akkor

g

is párhuzamos velük (2. ábra). Ezzel a (

*

) állítást beláttuk.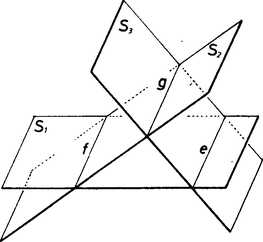

2. ábra

Térjünk most rá eredeti feladatunkra! A

P_{11}

és a

P_{13}

pontok rajta vannak az

a_{1}

egyenesen, a

P_{22}

és a

P_{32}

pontok pedig a

b_{2}

egyenesen. Az

a_{1}

és

b_{2}

egyenesek egy síkban vannak, mert a

P_{12}

pontban metszik egymást. Ekkor viszont a

P_{11} P_{22}

és a

P_{13} P_{32}

egyenesek is egysíkúak, mert mindkettő benne van az

a_{1}

és a

b_{2}

egyenesek által meghatározott síkban (3. ábra).

3. ábra

Ugyanígy láthatjuk be, hogy a

P_{13} P_{32}

és a

P_{23} P_{31}

egyenesek benne vannak az

a_{3}

és a

b_{3}

egyenesek által meghatározott síkban, a

P_{23} P_{31}

és a

P_{11} P_{22}

egyenesek pedig az

a_{2}

és a

b_{1}

egyenesek által meghatározott síkban. Másfelől a

P_{11} P_{22}

P_{13} P_{32}

P_{23} P_{31}

egyenesek nincsenek egy síkban, mert akkor az

a_{1}

a_{2}

a_{3}

egyenesek is egy síkban lennének. A szóban forgó 3 egyenes tehát kielégíti a (

*

) állítás feltételeit, ahonnan pedig így feladatunk állítása következik.

Megjegyzések. 1. A megoldásban szereplő (

*

) állítás nemcsak három egyenesre, hanem tetszőleges számú egyenesre is igaz: Ha a térben

n

db egyenes közül semelyik három nincs egy síkban, de bármely kettő egysíkú, akkor az egyenesek vagy egy pontban találkoznak, vagy pedig párhuzamosak.

2. A feladatunkban szereplő konfigurációra példát készíthetünk az F. 2582. feladat megoldását (1986. évi 10. szám, 436‐438. oldal) felhasználva. Az ottani II. megoldásban megmutattuk, hogy ha egy kocka három kitérő éle az

a_{1}

a_{2}

a_{3}

egyenes, akkor az egyes élek felezőpontján átmenő egyenesek közt van olyan, amelyik a másik két él egyenesét is metszi. Könnyen belátható ‐ a bizonyítást az olvasóra hagyjuk, ‐ hogyha ezeket az egyeneseket a 4. ábrán látható módon jelöljük

b_{1}

b_{2}

b_{3}

-mal, akkor a keletkező

P_{11} P_{22}

P_{13} P_{32}

P_{23} P_{31}

egyenesek párhuzamosak.

4. ábra