Kezdőlap


Feladat:	Gy.2372	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Kőrössi Attila , Szabó Tibor
Füzet:	1987/április, 168 - 170. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Geometriai egyenlőtlenségek, Tengelyes tükrözés, Pont körüli forgatás, Háromszögek nevezetes tételei, Magasságvonal, Terület, felszín, Szabályos sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1986/november: Gy.2372

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Mivel a háromszögek középpontja egybeesik, a két háromszög csúcsai ugyanazon a körön helyezkednek el. Rögzítsük az egyik háromszöget. Ekkor a másik háromszög csúcsai egyenként a kör kerületének 1/3 részén helyezkedhetnek el.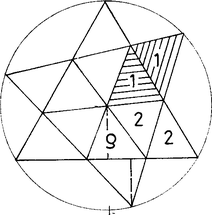

1. ábra

Az 1. ábrán látható módon minden, a közös részből kimaradó, külső háromszöghöz rendeljünk egy "belső'' háromszöget! Mivel egy belső-külső háromszög pár egyik oldala közös, a területük aránya megegyezik a közös oldalhoz tartozó magasságuk arányával. A belső háromszög magassága állandó ‐ megegyezik a szabályos háromszögekbe írható kör sugarával ‐, míg a külső háromszög magassága akkor a legnagyobb, amikor a harmadik csúcsa a körív felezőpontján van. Ekkor a külső háromszög egybevágó a belsővel, tehát magasságuk egyenlő. Ezért a külső háromszög magassága legfeljebb akkora, mint a megfelelő belső háromszög magassága.
Így a külső háromszögek területének

T_{k}

összege legfeljebb akkora, mint a belső háromszögek területének

T_{b}

összege,

T_{k} ≦ T_{b}

. Másrészt

T_{b}

éppen a háromszögek közös részének a területe, tehát

2 T_{b} + T_{k}

a két szabályos háromszög területének összege. Ezért:

2 = 2 T_{b} + T_{k} ≦ 2 T_{b} + T_{b} = 3 T_{b},

ahonnan kapjuk, hogy

2 / 3 ≦ T_{b} .

Ez pedig éppen a bizonyítandó állítás.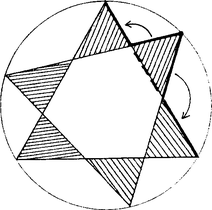

II. megoldás. A közös részből kimaradó ‐ a 2. ábrán vonalkázott ‐ háromszögek egybevágóak, mert forgatással, illetve tengelyes tükrözéssel egymásba vihetők. Az ábra alapján az is nyilvánvaló, hogy e háromszögek kerülete állandó, megegyezik az eredeti szabályos háromszögek egy oldalával.

2. ábra

Ismert, hogy adott kerületű háromszögek körül a szabályos háromszögnek van a legnagyobb területe. (Ennek bizonyítása megtalálható pl. Kazarinoff: Geometriai egyenlőtlenségek c. könyvének 57‐58. oldalán.) Ez azt jelenti, hogy a kimaradó rész területe akkor maximális, amikor a háromszögek egymáshoz képest

60^{\circ}

-kal vannak elforgatva.

3. ábra

A 3. ábrán látható, hogy ebben az esetben a közös rész feldarabolható 6 db, a levágott háromszögekkel egybevágó szabályos háromszögre, az eredeti háromszög pedig 9 db részháromszöget tartalmaz. Ebben az esetben tehát a közös rész területe

\frac{6}{9} = \frac{2}{3}

, minden más esetben pedig ennél nagyobb.
Ezzel az állítást beláttuk.