Kezdőlap


Feladat:	Gy.2369	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Pór Attila
Füzet:	1987/április, 167 - 168. oldal		PDF \| MathML
Témakör(ök):	Indirekt bizonyítási mód, Sakktáblával kapcsolatos feladatok, Sokszög lefedések, Gyakorlat
Hivatkozás(ok):	Feladatok: 1986/november: Gy.2369

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A tábla legfelső sorában levőket kivéve minden egyes fedetlen mezőhöz rendeljük hozzá azt a dominót ‐ ha van ilyen ‐, amelyik ennek a fedetlen mezőnek a fölső szomszédját fedi le. Ha nincs ilyen dominó ‐ azaz egy fedetlen mező fölső szomszédja nincs lefedve ‐, akkor nyilván készen vagyunk.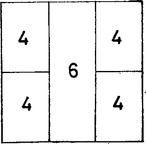
Vegyük észre, hogy ha ilyen módon két mezőhöz ugyanazt a dominót rendeljük, akkor ez a két üres mező szomszédos, és így itt újabb dominót helyezhetünk el. Föltehető tehát, hogy a fenti megfeleltetés kölcsönösen egyértelmű, azaz a tábla "alsó'' $6 \times 5$ -ös részébe eső fedetlen mezők mindegyikéhez rendel dominót, és különböző fedetlen mezőkhöz különböző dominót rendel.
Ez azt jelenti, hogy a tábla "felső'' $6 \times 5$ -ös részén legalább annyi dominó van, ahány fedetlen mező az alsó $6 \times 5$ -ös részen. Ha most az összesen 14 fedetlen mezőből 3-nál több van a legfelső sorban, akkor ezek között vannak szomszédosak és így ismét készen vagyunk. Abban az esetben pedig, ha legalább 11 fedetlen mező van az alsó $6 \times 5$ -ös részen, az ezekhez rendelt 11 dominó a tábla felső $6 \times 5$ -ös részén van. Mivel pedig összesen 11 dominó van a táblán, ilyenkor a legalsó sor teljesen üres, itt akár három újabb dominó is elfér.
Ezzel a bizonyítást befejeztük.

II. megoldás. Tegyük föl, hogy az állítás nem igaz, vagyis elhelyezhető 11 dominó a táblán úgy, hogy egyetlen újabb sem fér már el. Tekintsünk egy, a tábla csúcsához illeszkedő

2 \times 3

-as téglalapot (1. ábra). Ez a rész legalább egy dominót a belsejében tartalmaz, máskülönben a két, * -gal jelölt mező fedetlen volna. Ekkor viszont az e dominó által le nem fedett négy mezőből még legalább kettőt le kell fednünk ahhoz, hogy ebben a

2 \times 3

-as részben ne lehessen újabb dominót elhelyezni.

1. ábra

2. ábra

A tábla négy csúcsánál létrejövő négy ilyen téglalapban tehát összesen legalább 16 fedett mező van (2. ábra), így a középső

2 \times 6

-os sávban legfeljebb 6 mező lehet lefedve. Ennél kevesebb viszont nem lehet, ugyanis akkor az ide eső 6 szomszédos pár valamelyikében mindkét mező fedetlen maradna.
A 11 dominót tehát csak úgy helyezhettük el, hogy a négy saroktéglalapban pontosan 4‐4, a középső

2 \times 6

-os sávban pedig pontosan 6 fedett mező van. Ez utóbbi 6 mező közt nyilván nem lehetnek szomszédosak, így valamennyit különböző dominók fedik le és ezek "vízszintesen'' állnak.
Ugyanígy kapjuk, hogy legalább 6 "függőleges'' állású dominó is kell a táblára, de ez nem lehet, hiszen csak 11 dominónk van.
A kapott ellentmondás azt jelenti, hogy a kiinduló feltevésünk hamis, 11 dominót nem lehet úgy elhelyezni a táblán, hogy ne férne el még egy tizenkettedik is.

Megjegyzés. A 3. ábra mutatja, hogy 12 dominóra már nem igaz a feladat állítása.

3. ábra