| Feladat: | Gy.2365 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Benczúr P. , Bíró 100 A. , Csanádi P. , Csordás Z. M. , Dédesi P. , Elbert Judit , Fleiner T. , Kondacs A. , Pásztor 625 G. , Peller Z. , Radályi B. , Siklér F. , Sustik M. , Takách G. , Tornyi L. | ||
| Füzet: | 1987/május, 209 - 212. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Beírt alakzatok, Kombinatorikus geometria térben, Szabályos testek, Szabályos tetraéder, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1986/október: Gy.2365 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Vizsgáljuk meg, hol lehetnek a kocka csúcsai. A tetraéder élén nem lehet a kockának csúcsa, mert ekkor a kocka két, egymással hegyesszöget bezáró sík ‐ a tetraéder két szomszédos lapsíkja ‐ által meghatározott térrészben lenne úgy, hogy a síkok metszésvonalán is volna pontja, ez pedig nem lehetséges. Ennek a szemlélet alapján nyilvánvalónak tűnő állításnak a bizonyítását ‐ annak hosszadalmas volta miatt ‐ elhagyjuk. Az olvasó kísérelje meg önállóan elvégezni a bizonyítást. 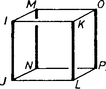 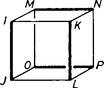 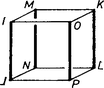 Megmutatjuk, hogy a két lap metszésvonala, a egyenes, párhuzamos a kocka és éleivel. Az és a egyenesek benne vannak az síkban, tehát nem lehetnek kitérőek. Az és a egyeneseknek nem lehet közös pontja, mert ha ilyen pont lenne, akkor benne lenne az egymástól különböző és síkokban is ‐ mint az illetve a egyenes pontja ‐, vagyis rajta lenne a két sík metszésvonalán. Ez viszont nem lehet, mert az és a egyenesek párhuzamosak. Most nézzük meg, hogy a másik két tetraéderlapon levő élek milyenek lehetnek. Tudjuk, hogy az , , , éleknek a kockában nincs közös csúcsuk; ezért ezek az élek csak az 1. ábrán látható esetek egyikével megegyező módon helyezkedhetnek el. Számunkra ebből most csak az a fontos, hogy a másik két tetraéderlapra illeszkedő kockaélek is párhuzamosak. Ekkor viszont az előzőhöz hasonló gondolatmenettel beláthatjuk, hogy a kocka és élei a tetraéder élével párhuzamosak. Mivel és ‐ mint a szabályos tetraéder két kitérő éle ‐ egymásra merőleges, ezért a kockaélek a tetraéder lapjain csak az 1/b ábrán látható módon helyezkedhetnek el. Mivel az sík párhuzamos az síkkal és nem metszi -t, nem metszi -t, ezért mindkettő párhuzamos azzal az egyértelműen meghatározott e síkkal, ami átmegy -n és nem metszi -t (2. ábra).   Tekintsük a tetraéder merőleges vetületét az síkon (3.ábra). A tetraéder képe az négyzet, a kocka képe az négyzet Az sík a tetraédert egy téglalapban metszi, ennek képe a téglalap, az sík és a tetraéder metszetének képe pedig a téglalap. A kocka képe éppen a és téglalapok metszete, tehát a metszetnek négyzetnek kell lennie, vagyis a két téglalap egybevágó. Ez azt jelenti, hogy az sík ugyanolyan messze van a éltől, mint az sík az éltől. Ha a két síkot egymás felé mozgatjuk úgy, hogy a -től, illetve -től való távolságuk mindig egyenlő, akkor távolságuk csökkenésével nőni fog az általuk az előbbiek alapján meghatározott négyzet oldala. Ezért lesz egy olyan egyértelműen meghatározott állapot, amikor a két sík távolsága megegyezik az négyzet oldalával, vagyis amikor az test kocka. Tehát egyértelműen létezik olyan kocka, amelynek csúcsai közül a tetraéder minden lapjára esik. 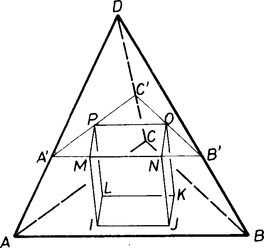 2. A másik esetben a tetraéder egyik lapján 4 csúcsa van a beírt kockának. Legyen ez a lap . A 4 kockacsúcs a kocka egyik lapjának 4 csúcsa kell hogy legyen, különben az sík metszené a kockát, ami lehetetlen. Legyen ez a 4 csúcs , , , , a kocka másik négy csúcsa pedig sorra , , , . Tekintsük az síknak a tetraéderrel vett metszetét. Ez egy szabályos háromszög, mert az sík párhuzamos a szabályos tetraéder lapjával, és az négyzet minden csúcsa ennek a háromszögnek a kerületén van. Ez csak az 5. ábrán látható, egyértelműen meghatározott esetben lehet. Tehát az metszet (szimmetriától eltekintve) egyértelműen meghatározza az , , , pontokat, és ezek merőleges vetületeként az , , , pontokat. Általános esetben ezek a pontok egy négyzetes hasáb csúcsai lesznek, és az sík egyetlen helyzetében lesz ez a hasáb kocka. Tehát ebben az esetben is egyetlen kocka van, ami a tetraéderbe írható. Ezek után rátérünk a kockák élhosszának kiszámítására.  Először a második esetet vizsgáljuk. A tetraéder élhossza legyen egységnyi. Ekkor a tetraéder testmagassága A 4. és az 5. ábra jelöléseit használva : Mivel a háromszög szabályos, így legyen a kocka éle ekkor A háromszög szabályos, így amiből tehát
Tehát a kocka éle ebben az esetben : Az első esetben szintén legyen a tetraéder élhossza és jelölje a kocka élhosszát, az síknak -től vett távolságát. Nyilván ugyanez a lesz az síknak a -től vett távolsága (a 2. ábra jelöléseivel). Legyen az és egyenesek távolsága, ami nem más, mint felezőpontjaik ‐ illetve ‐ távolsága. Mivel az háromszög derékszögű, így Pitagorasz tételéből és mivel , ezért Másrészt nyilván tehát
Ha a 2. ábrán meghosszabbítjuk az és egyeneseket az és szakaszokig, akkor a kapott szakasz hosszára igaz a következő aránypár: De , , , így Ezt (2)-be beírva így a kocka éle ebben az esetben |