Feladat: Gy.2357 Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1987/március, 113 - 114. oldal  PDF  |  MathML 
Témakör(ök): Középpontos tükrözés, Kocka, Térbeli ponthalmazok távolsága, Térbeli szimmetrikus alakzatok, Gyakorlat
Hivatkozás(ok):Feladatok: 1986/szeptember: Gy.2357

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Megmutatjuk, hogy az SA és az SG síkok harmadolják a kocka AG testátlóját, és így a távolságuk 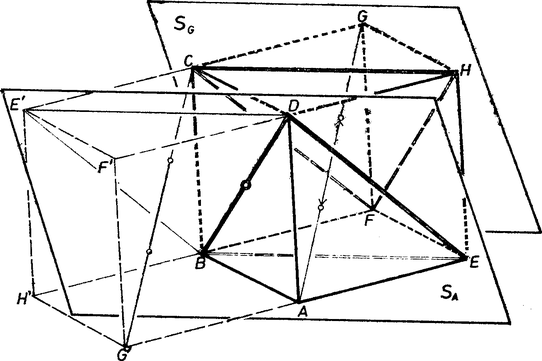AG3=3/3.
Az AG átló körüli 120°-os forgatások a kockát önmagába viszik át. E forgatások során ezért az SA és az SG síkok önmagukba mennek át, tehát mindkét sík merőleges az AG testátlóra. A szimmetria miatt a G pontnak az SG síktól való távolsága megegyezik az A pontnak az SA síktól való távolságával, ezért elegendő megmutatnunk, hogy például ez utóbbi távolság megegyezik az SA és SG síkok távolságával.

 
 
1. ábra
 

Tükrözzük a kockát a BD lapátló felezőpontjára. Így az eredetivel közös lapú ABCDG'H'E'F' kockát kapjuk (1. ábra). Az SA=EBD sík tükörképe önmaga, és így az A-nak az SA síktól mért távolsága egyenlő a tükörképpont és a tükörképsík, azaz a C pont és az SA sík távolságával. Ez utóbbi viszont éppen az SA és az SG síkok távolsága, hiszen a C pont benne van az SG síkban. Ezzel a bizonyítást befejeztük.
 

II. megoldás. Betűzzük a kocka csúcsait az 1. ábra szerint, és tekintsük az A kezdőpontú, A-val szomszédos csúcsokba mutató AB→, AD→ és AE→ vektorokat (2. ábra).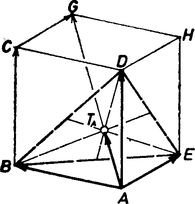
 
 
2. ábra
 

Ismeretes, hogy ekkor az EBD háromszög TA súlypontjába mutató A kezdőpontú vektor a háromszög csúcsaiba mutató vektorok számtani közepe, ATA→=13(AB→+AD→+AE→). Másfelől nyilván AB→+AD→+AE→=AB→+BC→+CG→=AG→, azaz AG→=3ATA→.
A kapott egyenlőség azt jelenti, hogy az A,TA és a G pontok egy egyenesen vannak, továbbá a TA pont‐ és így az SG sík ‐ harmadolja az AG szakaszt. Ugyanez természetesen az SG síkra is igaz. Mivel pedig az AG testátló merőleges az SA és az SG síkokra, a két sík távolsága a testátló harmada, 3/3.
 
Megjegyzés. Mindkét megoldásban csak a szóban forgó síkok és a testátló merőlegességének bizonyításához volt szükség a kocka speciális tulajdonságaira (3-adrendű forgásszimmetria), így a megoldások általában azt adják, hogy egy testátló két végpontjával szomszédos csúcsokon átmenő síkok minden paralelepipedonban harmadolják a testátlót.