Feladat: Gy.2348 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Beke T. ,  Benczúr A. ,  Bereczky Á. ,  Binder Zsuzsanna ,  Bíró 100 A. ,  Bukszár J. ,  Csáki Cs. ,  Csott R. ,  Cynolter G. ,  Dringó L. ,  Fajszi B. ,  Fleiner T. ,  Grallert Krisztina ,  Hantosi Zs. ,  Janszky J. ,  Jinda B. ,  Károlyi Gy. ,  Kecskés K. ,  Kégl B. ,  Keleti T. ,  Kovács 666 T. ,  László A. ,  Máté Nóra ,  Pál G. ,  Pásztor 625 G. ,  Rimányi R. ,  Siklér F. ,  Sustik M. ,  Szalay Gy. ,  Szederkényi Judit ,  Tasnádi T. ,  Vasy A. ,  Zaránd G. 
Füzet: 1987/március, 111 - 112. oldal  PDF  |  MathML 
Témakör(ök): Vetítések, Indirekt bizonyítási mód, Terület, felszín, Egyéb sokszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1986/május: Gy.2348

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat állítását sokszög helyett tetszőleges K konvex síkidomra bizonyítjuk be.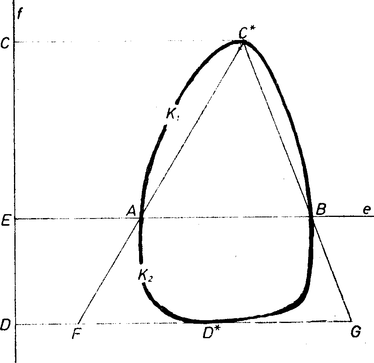
Messe K-t az e egyenes az A és B pontokban, és vágja K-t a feltétel szerint egyenlő területű K1 és K2 részekre. Ekkor K1 és K2 nyilván konvexek.

 
 

C* és D* legyenek a K1, illetve K2 részidomok kerületének olyan pontjai, amelyeknek az f egyenesen levő C és D merőleges vetületei által meghatározott CD szakasz alkotja a K síkidom vetületét az f egyenesen. Ha az A és B pontok f egyenesre vonatkozó ‐ e és f merőlegessége miatt közös ‐ merőleges vetületét E-vel jelöljük, akkor elegendő megmutatnunk, hogy CE:ED≦1+2, mert a C és D pontok szimmetriája miatt ebből DE:EC≦1+2 is következik.
Mivel K1 konvex, ezért az ABC* háromszög része K1-nek, vagyis területe legfeljebb akkora, mint K1 területe.
A merőleges vetítés miatt a DD* egyenes párhuzamos e-vel. Legyenek a DD* egyenes metszéspontjai a C*A, illetve C*B egyenesekkel F, illetve G. Megmutatjuk, hogy az AFGB trapéz tartalmazza a K2 részidomot. A K2 konvex, ezért teljes egészében az e egyenesnek a D*-ot tartalmazó oldalán helyezkedik el. Tegyük fel, hogy van olyan K2-beli P pont, amely nincs benne az AFGB trapézban! Ekkor K konvex volta miatt a C*P szakasz teljes egészében K-ban van, tehát az e egyenessel való Q metszéspontja is K-beli. Feltevésünkből viszont következik, hogy a Q pont nincs rajta az AB szakaszon. Ez ellentmondás, mert a konvex síkidomot az e egyenes egy szakaszban metszi, esetünkben A és B voltak ennek végpontjai. Az AFGB trapéz tehát valóban tartalmazza a K2 részidomot, így annak területe legfeljebb akkora, mint a trapézé.
Mivel K1 és K2 egyenlő területűek, a C*AB háromszög területe legfeljebb akkora, mint az AFGB trapéz területe. Másképpen szólva a C*AB háromszög területe legfeljebb fele a hozzá középpontosan hasonló C*FG háromszög területének. Ez azt jelenti, hogy a C*AB háromszög AB oldalához tartozó magassága ‐ ami egyenlő a CE szakasszal ‐ legfeljebb 22 -ed része a C*FG háromszög FG oldalához tartozó magasságának, ami egyenlő a CD szakasszal. Tehát:
CE:ED=CE:(CD-CE)≦≦22⋅CD:(1-22)⋅CD==22:(1-22)=1+2.



Ezzel az állítást beláttuk.
 

Megjegyzés. Látható a bizonyításból, hogy ha a K síkidom megegyezik a C*FG háromszöggel, akkor a vetületszakaszok aránya éppen 1+2, tehát a feladat állítása tovább nem javítható.