Feladat: Gy.2343 Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1986/december, 449 - 450. oldal  PDF  |  MathML 
Témakör(ök): Nevezetes azonosságok, Egyenletek grafikus megoldása, Paraméteres egyenletek, Egyenletek, Egyenlőtlenségek, Polinomok szorzattá alakítása, Gyakorlat
Hivatkozás(ok):Feladatok: 1986/május: Gy.2343

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha n=1, akkor egyenletünk azonosság, ilyenkor tehát minden valós szám megoldás. A továbbiakban legyen n>1.
Két n-edik hatvány különbsége szorzattá alakítható. Ennek megfelelően (1)-ből

1=xn-(x-1)n=[x-(x-1)][xn-1+xn-2(x-1)+...+x(x-1)n-2+(x-1)n-1],


azaz
1=xn-1+xn-2(x-1)+...+x(x-1)n-2+(x-1)n-1.(2)

Ha x>1, akkor (2) jobb oldalán már az első tag is nagyobb 1-nél, a további tagok pedig pozitívak. Ezért (1)-nek nincs 1-nél nagyobb gyöke.
Ha x=1, akkor (1) mindkét oldalán 0 áll, így az 1 megoldása egyenletünknek.
Vezessük most be a t=1-x változót. Ezzel (1)-ből a t-re mint ismeretlenre a (-t)n=(-t+1)n-1 egyenletet kapjuk. Ha n páros, akkor ez a
tn=(t-1)n-1,(3)
ha pedig n páratlan, akkor rendezés után a
(t-1)n=tn-1(4)
alakot ölti. Vegyük észre, hogy az utóbbi esetben t-re éppen az eredeti, (1) egyenletet kaptuk. Ezért páratlan n-re egyrészt megoldás a t=1 alapján kapott x=0, másrészt, mivel a fentiek szerint (4)-nek nincs olyan megoldása, amire t=1-x>1, páratlan n-re (1)-nek nincs x<0 megoldása.
Legyen az n továbbra is páratlan. Tisztáznunk kell még, van-e gyöke (1)-nek a (0,1) nyílt intervallumban. A tagadó válasz például (2) jobb oldalának behatóbb vizsgálatából is kiderül, egyszerűbben kapjuk azonban az ilyenkor nyilván teljesülő
(x-1)n>x-1>xn-1

egyenlőtlenségből. Ezzel az 1-nél nagyobb páratlan kitevők esetét teljes egészében tisztáztuk.
Páros n-re azt állítjuk, hogy (1)-nek nincs 1-nél kisebb gyöke sem, vagy ami ezzel ekvivalens, (3)-nak nincs pozitív megoldása. Valóban, ha 0<t<1, akkor |t-1|<1, így (3) jobb oldala negatív, a bal oldal pedig nem az. Végül ha t≧1, akkor t>t-1≧0, így tn>(t-1)n, tehát továbbra is (3) bal oldala a nagyobb.
Összefoglalva, ha n=1, akkor (1)-nek minden valós szám gyöke. Ha n>1 és páros, akkor (1) egyetlen megoldása x=1; ha pedig n>1 és páratlan, akkor (1)-nek két megoldása van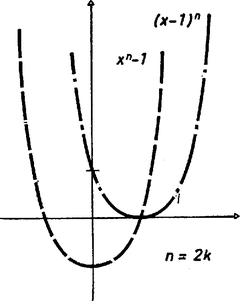: x1=1 és x2=0.
 
Megjegyzés. A talált eredmények megsejthetők az f(x)=(x-1)n és a g(x)=xn-1 függvények grafikonjának fölvázolása alapján ‐ mindkettő egységnyi eltolással származtatható az xn hatványfüggvény grafikonjából, előbbi az x, utóbbi pedig az y tengellyel párhuzamosan (1 ‐ 2. ábrák).
 
 
1. ábra
 

 
 
2. ábra
 

Több dolgozat páros n-re "parabolának'' nevezte a szóban forgó görbéket, és még a megoldásban is hivatkoztak erre, mondván, hagy "egyállású egybevágó paraboláknak nem lehet egynél több metszéspontjuk''. Általános esetben mind az elnevezés, mind pedig az indoklás hibás (bár a konklúzió jelen esetben helyes), a görbék csak az n=2 esetben parabolák.