Kezdőlap


Feladat:	Gy.2340	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Csott R. , Cyonolter G. , Hantosi Zs. , Illés L. , Illés T. , Janszky J. , Pál G. , Rozgonyi T. , Sustik M. , Szabó 639 A. , Szalay Gy. , Tasnádi T. , Vasy A. , Veres E.
Füzet:	1987/április, 158 - 160. oldal		PDF \| MathML
Témakör(ök):	Húrnégyszögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1986/április: Gy.2340

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat állítása csak a következő módosított formában igaz: Az $A_{1}$ , $A_{2}$ , $A_{3}$ , $A_{4}$ pontok pontosan akkor vannak egy körön vagy egyenesen, ha a $B_{1}$ , $B_{2}$ , $B_{3}$ , $B_{4}$ pontok egy körön vagy egyenesen vannak (1. ábra). Ezt a módosított állítást bizonyítjuk.

1. ábra

A megoldás során "szögön'' mindig előjeles szöget értünk. A

P Q R ∢

legyen pozitív, ha a

P Q R

háromszöget pozitív irányban körüljárva, a csúcsok sorrendje

P, Q, R

; ha pedig a csúcsok sorrendje

P, R, Q

, akkor a

P Q R ∢

legyen negatív (2. ábra).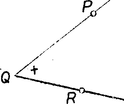

2. ábra

Ha a

P

Q

R

pontok egy egyenesen vannak, akkor a

P Q R ∢

legyen 0. Ennek a jelölésnek a segítségével egyszerűen kifejezhetjük azt, hogy a

P

Q

R

S

pontok mikor vannak egy körön vagy egyenesen. Felhasználva, hogy egy négyszög pontosan akkor húrnégyszög, ha egyik oldala a másik két csúcsból ugyanolyan előjeles szögben látszik, vagy ha szemközti előjeles szögeinek különbsége

\pm 180^{\circ}

(3. ábra), kapjuk hogy:

A

P

Q

R

S

pontok pontosan akkor vannak egy körön vagy egyenesen, ha

\begin{matrix} P Q R ∢ - P S R ∢ = k \cdot 180^{\circ}, \end{matrix}

(1)

ahol k egész szám.

3a) ábra

3b) ábra

A bizonyítás során az előjeles szögeknek két további nyilvánvaló tulajdonságát is fel fogjuk használni:

\begin{matrix} P Q R ∢ = - R Q P ∢, & (2) \\ P Q R ∢ + R Q S ∢ = P Q S ∢ . & (3) \end{matrix}

A fenti előkészületek után állításunk bizonyítása számolássá egyszerűsödik. Mivel az

A_{1}

A_{2}

B_{1}

B_{2}

pontok mindegyike rajta van a második körön, ezért van olyan

k_{2}

egész szám, amelyre (4. ábra):

\begin{matrix} A_{1} A_{2} B_{2} ∢ - A_{1} B_{1} B_{2} ∢ = k_{2} \cdot 180^{\circ} . \end{matrix}

(4)

4. ábra

Ugyanígy kapjuk, hogy vannak olyan

k_{3}

k_{4}

k_{1}

egészek, amelyekre:

\begin{matrix} B_{2} A_{2} A_{3} ∢ - B_{2} B_{3} A_{3} ∢ = k_{3} \cdot 180^{\circ}, & (5) \\ A_{3} A_{4} B_{4} ∢ - A_{3} B_{3} B_{4} ∢ = k_{4} \cdot 180^{\circ}, & (6) \\ B_{4} A_{4} A_{1} ∢ - B_{4} B_{1} A_{1} ∢ = k_{1} \cdot 180^{\circ} . & (7) \end{matrix}

Adjuk össze a (4)‐(7) egyenleteket, majd a bal oldalt (2) és (3) felhasználásával alakítsuk át!

\begin{matrix} (A_{1} A_{2} B_{2} ∢ + B_{2} A_{2} A_{3} ∢) + (A_{3} A_{4} B_{4} ∢ + B_{4} A_{4} A_{1} ∢) - \\ - (B_{4} B_{1} A_{1} ∢ + A_{1} B_{1} B_{2} ∢) - (B_{2} B_{3} A_{3} ∢ + A_{3} B_{3} B_{4} ∢) = \\ = (A_{1} A_{2} A_{3} ∢ - A_{1} A_{4} A_{3} ∢) + (B_{2} B_{1} B_{4} ∢ - B_{2} B_{3} B_{4} ∢) = \\ = (k_{1} + k_{2} + k_{3} + k_{4}) \cdot 180^{\circ} . \end{matrix}

Az egyenletnek ebből az alakjából az (1) állítást felhasználva közvetlenül adódik a bizonyítandó állítás.

Megjegyzések. 1. Az előjeles szögekkel való számolás azért volt célszerű, mert így elkerültük a bonyolult esetszétválasztást.
2. Nagyon sok megoldó elkövette azt a hibát, hogy csak a 4. ábrán látható esetben bizonyította az állítást.
3. A feladatban szereplő állítást Miquel-tételnek nevezik (lásd pl. Molnár Emil: Matematikai versenyfeladatok gyűjteménye 1947‐70. című könyvének 566. oldalán).
4. Feladatunk eredményét, valamint a sztereografikus projekció tulajdonságait (lásd p1. Reiman István: A geometria és határterületei c. könyvének 362. oldalát) felhasználva egyszerűen bizonyítható a következő térgeometriai állítás :
Legyenek az

A

B

C

D

A^{'}

B^{'}

C^{'}

D^{'}

olyan pontok egy gömbön, hogy az

A B C D

A B A^{'} B^{'}

B C B^{'} C^{'}

C D C^{'} D^{'}

D A D^{'} A^{'}

pontnégyesek egysíkúak, azaz a felsorolt 5 pontnégyes egy-egy, az adott gömbre illeszkedő körön van. Ekkor az a négy pont (

A^{'}

B^{'}

C^{'}

D^{'}

), amelyeken a fenti öt kör közül csak kettő- kettő halad át, szintén egy körön van, azaz egysíkú (5. ábra).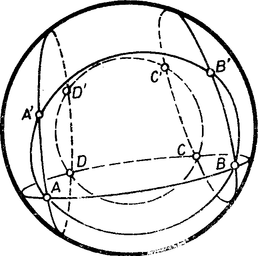

5. ábra

Az állítás másképpen azt mondja, hogy ha olyan, adott gömbbe írt hatlapú konvex testet akarunk építeni, amelynek lapjai négyszögek, akkor amennyiben a test öt lapját úgy vesszük föl, hogy a csúcsok a gömb felszínére illeszkednek, az öt lap által határolt térrész ("a nyitott doboz") egy síknégyszöggel lezárható (6. ábra).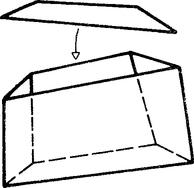

6. ábra

A gömb egy tetszőleges pontját választva a projekció pólusának, a bizonyítandó állítás éppen feladatunk állítása lesz.