Feladat: Gy.2337 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Benczúr András [1983-1987] ,  Csáki Cs. ,  Csűrös M. ,  Szabó 639 A. 
Füzet: 1987/február, 69 - 72. oldal  PDF  |  MathML 
Témakör(ök): Egyenletrendszerek grafikus megoldása, Mozgással kapcsolatos szöveges feladatok, Gyakorlat
Hivatkozás(ok):Feladatok: 1986/április: Gy.2337

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az áttekinthetőség kedvéért legyen S=84, az út hossza. A három gyerek útjának összege így legalább 3S ‐ több is lehet, ha nem csak előre mozognak ‐ és ha a gyalogszerrel megtett utak összege legalább S ‐ ami mindig igaz, ha üres bicikli nem vontatható ‐, akkor van olyan gyerek, aki az útnak legalább az egyharmadán gyalogol, és így neki legalább 1/3⋅S:5+2/3⋅S:20=S/10=8,4 órára van szüksége a célba jutáshoz. Láttuk a 2289. gyakorlat megoldásában, hogy ennyi idő már elegendő.*

 

A fentiek szerint az új feltétel ‐ üres bicikli vontatása ‐ csak úgy teheti lehetővé a felhasznált idő csökkentését, ha a gyalogosan megtett utak összege S-nél kevesebb. Ilyenkor vannak az útnak olyan részei, ahol senki sem gyalogol. Vizsgáljuk most az ilyen utazásokat, azaz legyen a gyalogosan megtett utak összege αS, ahol 0≦α<1. Ilyenkor legalább (1-α)S hosszúságú útszakaszon mindhárman biciklizve jutnak át ‐ hívjuk biciklis szakaszoknak az út ilyen részeit.
Vizsgáljuk meg, hogy a biciklik és a gyerekek külön-külön legalább mennyi időt töltenek az úton. Bár a feladat csak a gyerekek célba jutását írja elő, nyilván föltehető, hogy a kerékpárok is eljutnak a célba.
 

A biciklis szakaszok minden B pontján tehát kerékpáron jutnak át a gyerekek. Mivel csak két bicikli van, ezért egyikük nyergében legalább ketten haladnak át a B ponton, ami azt jelenti, hogy ennek a biciklinek üresen visszafelé is át kell haladnia B-n. Mivel önállóan nem közlekedhet és itt senki nem gyalogol, a másik biciklinek kell visszafelé vontatnia, és ez most lehetséges is. Miután pedig a biciklik végül célba érnek, a két biciklinek újra át kell jutnia B-n, immár előre mozogva.
 

A biciklis szakaszokon tehát mindkét kerékpár legalább háromszor halad át, kétszer előre, egyszer pedig visszafelé. Tudjuk emellett, hogy a biciklik a gyalogutakon is átjutnak, ezért külön-külön legalább αS+3(1-α)S=(3-2α)⋅S utat tesznek meg. Ehhez pedig legalább (3-2α)S:20 órára van szükség.
 

Próbáljuk most megbecsülni a gyerekek által felhasznált idők összegét. Az összesen 3S hosszúságú útból α⋅S utat gyalog, a fennmaradó (3-α)S utat pedig biciklizve teszik meg a gyerekek. Láttuk ugyanakkor, hogy a biciklis szakaszokon egy biciklistának visszafelé is el kell haladnia ‐ a másik, üres biciklit vontatva ‐ és így ő ezt a szakaszt előre mozogva is kétszer teszi meg.
 

A gyerekek biciklin megtett útjának összege ezért valójában a (3-α)S ,,tiszta'' előre mozgásnál a biciklis szakaszoknak legalább a kétszeresével több, azaz legalább (3-α)S+2(1-α)S=(5-3α)S.
 

A gyerekek utazással töltött idejének összege így legalább αS5+(5-3α)S20=(5+α)S20. Van tehát a három gyerek között olyan, aki ennek az időnek legalább az egyharmadát, (5+α)S60 órát tölt az úton.
A célba jutáshoz szükséges idő így a biciklik miatt legalább (3-2α)S20 óra, a gyerekek miatt pedig legalább (5+α)S60 óra.
 
 
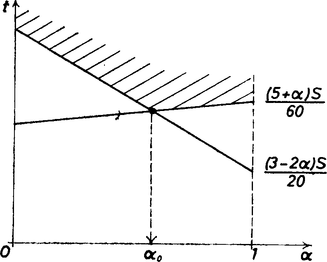1. ábra
 

Ábrázoljuk a kapott alsó korlátokat az α függvényében (1. ábra). Ekkor a lehetséges (α,t) párok a satírozott tartományban helyezkednek el. A két határoló egyenes meredeksége ellenkező előjelű, a tartomány ,,legmélyebb'' pontja tehát a határoló egyenesek metszéspontja, amelynek α0 abszcisszája a (3-2α)S20=(5+α)S60 egyenlet megoldásával α0=47.
A gyerekek célba jutásához így legalább 3-2α020S=5+α060S=13140S=7,8 óra szükséges. Ez kevesebb, mint a 2289. gyakorlatban kapott 8,4 óra, de meg kell mutatnunk, hogy meg is valósítható.
A fentiekből kiolvasható, hogy erre úgy kerülhet sor, ha a gyalogosan megtett utak összege 47S.
Jelöljük ki az AB=S hosszúságú úton a T1 és T2 pontokat úgy, hogy AT1=T2B=27S legyen (2.ábra).
 
 
2. ábra
 

Induljon az A-ból egy gyerek gyalog, a másik kettő pedig biciklivel. A T2 pontban az egyik biciklista szálljon le és gyalogoljon tovább a B felé, társa pedig az üres biciklit vontatva forduljon vissza. Mire a T1-be ér, összesen AT2+T2T1=87S utat tesz meg, és így a negyedakkora sebességgel kezdettől gyalogló harmadik eddigre 27S=AT1 út után éppen ideér. Késedelem nélkül felülhet tehát a visszahozott kerékpárra, és mindketten egészen a célig biciklizhetnek. Az is látszik, hogy ekkor a T2-ben elhagyott gyaloglóval egy időben érnek az út végére, hiszen az elválás után az a még hátralevő T2B=27S utat éppen annyi idő alatt teszi meg, mint biciklit vontató társa a négyszer akkora T2T1+T1B=87S utat. (A 2. ábrán szaggatott és folytonos szakaszok jelzik a gyalogosan, illetve biciklivel megtett útszakaszokat.)
Ilyen körülmények között tehát mindhárman egyszerre érnek célba, az elhasznált idő pedig nyilván 27S:5+57S:20=13140S=7,8 óra.
A három gyerek tehát 7,8 óra alatt eljuthat a célba, ennél rövidebb idő alatt viszont nem.
 

Megjegyzések. 1. Látható, hogy nem a fenti az egyetlen olyan útiterv, amely biztosítja, hogy éppen 7,8 óra alatt érjenek célba a gyerekek. Újabb lehetőségeket kapunk, ha szakaszokra osztjuk az AB utat és minden egyes szakaszon a fenti módszer szerint szervezzük meg az utazást.
2. Könnyű meggondolni, hogy az üres kerékpár vontatása akkor teszi lehetővé az utazáshoz szükséges idő rövidítését, ha a kerékpáros és a gyalogos sebességének az aránya nagyobb, mint 3. Ekkor érdemes ugyanis biciklis szakaszt közbeiktatni, hisz ezen még a visszaút árán is gyorsabban jutnak túl, mint gyalogszerrel.
* 1986. áprilisi szám, 170‐171. old.