Feladat: Gy.2333 Korcsoport: 18- Nehézségi fok: -
Füzet: 1986/december, 445 - 447. oldal  PDF  |  MathML 
Témakör(ök): Tengelyes tükrözés, Egyenes, Mértani helyek, Térelemek és részeik, Vektorok lineáris kombinációi, Gyakorlat
Hivatkozás(ok):Feladatok: 1986/március: Gy.2333

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A tér egy P pontja akkor és csak akkor tartozik a szóban forgó ponthalmazhoz, ha a két egyenes, a és b tartalmaz a P-re tükrös helyzetű pontokat, ami pontosan akkor teljesül, ha az a egyenes P-re vonatkozó a' tükörképének van a b-vel közös pontja. (Ilyenkor természetesen a b egyenes tükörképének is van közös pontja az 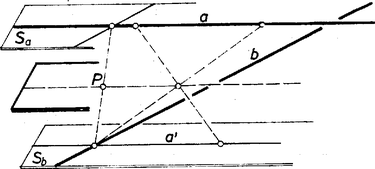a-val.)
Az a egyenes lehetséges tükörképei a térnek az a-val egyállású egyenesei. Minden egyes ilyen a' egyenesbe végtelen sok tükrözés viszi az a-t, ezek centrumai a két egyenes, a és a' középpárhuzamosát alkotják. Vegyük észre, hogy ekkor a és a' tengelyesen tükrösek az említett középpárhuzamosra.
A keresett ponthalmaz tehát az a-val egyállású egyenesekből, a lehetséges középpárhuzamosokból áll. Egy ilyen e egyenes akkor és csak akkor tartozik a keresett halmazhoz, ha az a egyenes e-re vonatkozó tükörképének van pontja a b-n.
A két adott egyenes, a és b kölcsönös helyzete szerint ezután három esetet különböztethetünk meg:
1. Ha a és b párhuzamosak, akkor b az egyetlen olyan, a-val párhuzamos egyenes a térben, amelynek van pontja b-n. Ennek megfelelően a keresett ponthalmaz is egyetlen egyenesből, az a és b középpárhuzamosából áll.
2. Ha a és b metszők, akkor a tér egy a-val egyállású a' egyenesének pontosan akkor van pontja b-n, ha a' benne van az a és b egyenesek S síkjában. Mivel pedig az S sík tetszőleges, a-val egyállású e egyenese középpárhuzamosa az a, illetve az a e-re vonatkozó a' tengelyes tükörképének, a keresett ponthalmaz maga az S sík.
3. Ha a és b kitérők, akkor a tér a-val egyállású, a b-vel közös ponttal rendelkező egyenesei az a-val párhuzamos, b-re illeszkedő Sb síkot alkotják. A keresett ponthalmaz ekkor az a és az Sb-beli, a-val párhuzamos egyenesek középpárhuzamosaiból áll. Ezek a középpárhuzamosok egy, az Sb-vel párhuzamos síkot alkotnak, amely nem más, mint az Sb és az a-n átmenő, b-vel ‐ és Sb-vel ‐ párhuzamos Sa sík középpárhuzamos síkja.

 
 

 
Megjegyzés. Az érkezett megoldások zöme ‐ érthetően ‐ könnyűség szempontjából sorra vette a és b kölcsönös helyzetének három típusát. Így azonban megszűnt a feladat egysége, három hasonló feladatot oldottak meg.
A föntiekben egy közös alapgondolatot bocsátottunk előre, mint ahogyan az alábbi megoldás is egységesen közelíti meg a feladatot.
 

II. megoldás. Legyen az a és b egyenes egy-egy pontja A, ill. B, az AB szakasz felezőpontja O, továbbá az egyenesek egy-egy irányvektora a, ill. b.
Ha C és D az a, illetve b egyenes tetszőleges pontjai, akkor egyértelműen léteznek olyan α és β valós számok, amelyekre:
OC→=OA→+αaésOD→=OB→+βb,
tehát ha a CD szakasz felezőpontját F-fel jelöljük, akkor:
OF→=12(OC→+OD→)=12(OA→+αa+OB→+βb)=12(αa+βb).

Itt a C és D pontok változtatásával α és β külön-külön minden valós értéket felvesz. Az OF→ tehát mindig benne van az O ponton átmenő, az a és b egyenesekkel párhuzamos síkban. Ha az a és b irányvektorok nem párhuzamosak, akkor ismeretes, hogy ennek az általuk meghatározott síknak minden F pontjához léteznek olyan α és β valós számok, hogy OF→=12(αa+βb), a keresett ponthalmaz tehát az O-n átmenő, a-val és b-vel párhuzamos sík. Az eddigiekben nem volt lényeges, hogy a és b kitérők vagy metszik egymást. Végül ha a és b párhuzamosak, akkor b=k⋅a és OF→=12(α+βk)a, a keresett ponthalmaz egyenessé egyszerűsödik, és az O-n átmenő, a-val és b-vel párhuzamos egyenes, a és b középpárhuzamosa adódik.
Ezzel a feladatot megoldottuk.
A megoldásból kiderül, hogy az O pont látszólag önkényes kiválasztásának nincs szerepe, hiszen bármely, a halmazhoz tartozó O pont esetén ugyanaz az O-n átmenő, a,b-vel párhuzamos sík, illetve egyenes adódik.