Feladat: Gy.2322 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Binder Zsuzsanna ,  Bíró 100 A. ,  Bobok G. ,  Bordás F. ,  Bősze P. ,  Bukszár J. ,  Buttyán L. ,  Csahók Z. ,  Csapdi M. ,  Dédesi P. ,  Domokos P. ,  Dutkó A. ,  Elek V. ,  Figeczky G. ,  Fleiner G. ,  Hahn Zsuzsa ,  Hídvégi Z. ,  Horváth 963 J. ,  Jinda B. ,  Keleti T. ,  Kovács 475 P. ,  Kun A. ,  Köröndi B. ,  Lois L. ,  Magyar 575 Cs. ,  Mándy A. ,  Máté Nóra ,  Mikusi Cs. ,  Novák Zs. ,  Pál Bernadett ,  Pásztor 625 G. ,  Petrik Z. ,  Rakaczi Zs. ,  Rimaszéki F. ,  Siklér F. ,  Sipos E. ,  Specziár A. ,  Szabó 522 B. ,  Szakállas Sz. ,  Tavaszi G. ,  Tőkei Zs ,  Tornyi L. ,  Török Zs. ,  Wolkensdorfer P. ,  Zsámboki A. 
Füzet: 1986/november, 391 - 392. oldal  PDF  |  MathML 
Témakör(ök): Geometriai egyenlőtlenségek, Indirekt bizonyítási mód, Hossz, kerület, Paralelogrammák, Rombuszok, Négyszögek geometriája, Gyakorlat
Hivatkozás(ok):Feladatok: 1986/február: Gy.2322

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy a feltételeknek eleget tevő négyszögek éppen a rombuszok. Legyen a négyszög ABCD, az átlók metszéspontja M. Mivel a négyszög konvex, ezért M a négyszög belsejében van.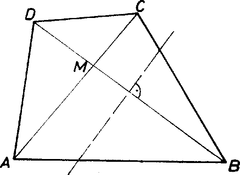

 
 

Tegyük fel, hogy M nem felezi a BD átlót, hanem, mondjuk, D-hez közelebb van, mint B-hez. Ekkor az A és C csúcsok közül valamelyik biztosan nincs rajta BD felező merőlegesén, mert ha mindkettő rajta lenne, akkor M felezőpont lenne. És mivel M az AC szakasz belső pontja, A és C közül az egyik ‐ mondjuk A ‐ vagy a felező merőlegesen, vagy annak D felőli partján fekszik. Ekkor MD<MB és DA≤BA, és így MD+DA+AM<MB+BA+AM, vagyis az MDA háromszög kerülete kisebb az MBA háromszög kerületénél ‐ ellentmondás!
Következésképp M-nek feleznie kell a BD átlót. Hasonlóan láthatjuk, hogy felezi az AC átlót is, amiből adódik, hogy négyszögünk paralelogramma, mert átlói felezik egymást. Legyenek a paralelogramma oldalai a és b, átlói pedig 2e és 2f hosszúságúak! Mivel az a, illetve b oldalra illeszkedő háromszögek kerülete egyenlő,
a+e+f=b+e+f
vagyis a=b. A négyszög ezért rombusz. Másrészt bármely rombuszt átlói négy egybevágó háromszögre bontanak, tehát a rombuszok eleget tesznek a feladat feltételeinek. Ezzel állításunkat beláttuk.
 

Megjegyzés. Nagyon sok dolgozatban csak annak bizonyítása szerepelt, hogy a négyszög szemközti oldalainak összege egyenlő, vagyis a négyszög érintőnégyszög. Mivel ennél jóval több is igaz, ezért ezek a dolgozatok 1 pontot kaptak.