Kezdőlap


Feladat:	Gy.2321	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Mándi Tibor
Füzet:	1986/november, 388 - 391. oldal		PDF \| MathML
Témakör(ök):	Függvények, Kombinatorikai leszámolási problémák, Kombinációk, Lottó, Klasszikus valószínűség, Gyakorlat
Hivatkozás(ok):	Feladatok: 1986/február: Gy.2321

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Előzetes megjegyzés. Kézenfekvőnek látszik ‐ és sokan próbálkoztak így ‐ annak összeszámolása, hogy hány esetben lesznek a kihúzott számok között szomszédosak. Ha $S$ jelöli a szóban forgó számötösök halmazát, akkor a keresett valószínűség $| S | / (\binom{90}{5})$ (itt $| S |$ az $S$ halmaz elemszámát jelöli), hisz az ilyenkor szokásos föltevés szerint bármely két számötös kihúzása egyformán valószínű.
Hogy ez az út milyen buktatókat rejt, azt egy beküldött dolgozat példáján mutatjuk be.
" $...$ a 90 darab számból 89 darab szomszédosakból álló párt tudok létrehozni. E kettő mellé még $(\binom{88}{3})$ -féleképpen választhatok további három számot, tehát összesen $89 \cdot (\binom{88}{3})$ olyan számötös van, amelyekben vannak szomszédos számok $...$ ''
Az elegáns gondolatmenet hibás, $S$ bizonyos elemeit ugyanis többször számolja meg. Az 1, 2, 3, 4, 5 például az (1, 2), a (2, 3), a (3, 4) és a (4, 5) párok révén négyszer is sorra kerül, hasonlóan az 1, 2, 5, 6, 9 kétszer, az 1, 2, 3, 4, 8 pedig háromszor. A szerző csak azokat az $S$ -beli elemeket számolta pontosan egyszer, amelyek éppen egy szomszédos számpárt tartalmaznak.
Az alábbiakban két megoldást mutatunk be. Először az $S$ alkalmas csoportosításával vázolunk egy összeszámolási lehetőséget, a tényleges leszámolást azonban egy szerencsés észrevétel segítségével némiképp módosítva végezzük el, és eközben a bizonyítás is alapvetően egyszerűsödik. A második megoldás során egy ravasz ötlettel közvetlenül jutunk el a végeredményhez.

I. megoldás. Csoportosítsuk az

S

elemeit aszerint, hogy legfeljebb hány szomszédos számot tartalmaznak, azaz legyen

S_{i}

(i = 2, 3, 4, 5)

azon számötösök halmaza, amelyekben előfordul

i

darab szomszédos szám, de

i + 1

már nem. A bevezetőben említett példáink közül 1, 2, 3, 4, 5 az

S_{5}

, 1, 2, 5, 6, 9 az

S_{2}

; végül 1, 2, 3, 4, 8 az

S_{4}

egy-egy eleme. Ekkor

S

a páronként közös elem nélküli

S_{2}

S_{3}

S_{4}

és

S_{5}

halmazok egyesítése. Elemszáma így az

S_{i}

-k elemszámának az összege.
Az alábbiakban kiszámoljuk az

S_{i}

halmazok elemszámát.
a)

S_{5}

elemeit öt szomszédos szám kihúzásakor kapjuk. Az öt szám legkisebbike egyértelműen határozza meg a szóban forgó számötöst, másrészt nyilván 1-tő1 86-ig változhat. Ennek megfelelően

| S_{5} | = 86

.
b) Egy

S_{4}

-beli számötös négy szomszédos elemének legkisebbike 87-féle lehet, az ötödik számot pedig a megmaradó 86 szám közül választhatjuk ki. Az így kapott

87 \cdot 86

lehetőség viszont

S_{5}

elemeit is tartalmazza, mégpedig mindegyiküket kétszer, az első, illetve a hátsó négyes kiválasztásakor. Így

| S_{4} | = 87 \cdot 86 - 2 \cdot | S_{5} | = 7310

.
c) Az előzőekhez hasonlóan

S_{3}

három szomszédos elemét 88-féleképpen, a további két elemet pedig

(\binom{87}{2})

-féleképpen választhatjuk ki. Így azonban ismét kapunk

S_{4}

, illetve

S_{5}

-beli elemeket. Az előbbieket kétszer, az utóbbiakat pedig háromszor számoltuk (1. ábra), így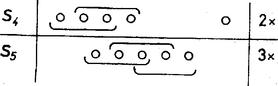

\begin{matrix} | S_{3} | = 88 \cdot (\binom{87}{2}) - 2 \cdot | S_{4} | - 3 \cdot | S_{5} | = 314 330. \end{matrix}

1. ábra

S_{2}

vizsgálatakor végképp elbonyolódni látszik a helyzet. A korábbiaknak megfelelően "bőven számolt''

89 \cdot (\binom{88}{3})

-féle számötös mindegyike a 2. ábra hat, páronként közös elem nélküli lehetőségének valamelyikébe tartozik. Újra többszörösen megkapjuk

S_{3}

S_{4}

és

S_{5}

elemeit, sőt bizonyos

S_{2}

-belieket (az ábrán

S_{21}

) is kétszer.
Az ábra jelöléseit használva

S_{21}

elemeit egyszer,

S_{22}

elemeit pedig kétszer számoljuk. Ismét megkapjuk

S_{3}

elemeit, az

S_{31}

-belieket kétszer, az

S_{32}

-belieket pedig háromszor. Végül

S_{4}

elemeire háromszor,

S_{5}

elemeire pedig négyszer kerül sor. Ennek megfelelően

\begin{matrix} | S_{2} | & = 89 \cdot (\binom{88}{3}) - | S_{22} | - 2 \cdot | S_{31} | - 3 \cdot | S_{32} | - 3 \cdot | S_{4} | - 4 \cdot | S_{5} | = \\ = 89 \cdot (\binom{88}{3}) - | S_{22} | - | S_{32} | - 2 \cdot | S_{3} | - 3 \cdot | S_{4} | - 4 \cdot | S_{5} | . \end{matrix}

| S_{2} |

fenti kifejezésében nem ismerjük

S_{22}

és

S_{32}

értékét, tehát azon számötösök számát, amelyek pontosan két szomszédos párt, és amelyek egy-egy szomszédos párt, illetve hármast tartalmaznak. Ezek az értékek egy kicsit másképpen, de némi ügyeskedéssel megkaphatók ‐ hasznos gyakorlatok az érdeklődő olvasó számára. Most azonban egy olyan lehetőséget mutatunk, amely alkalmas a hat csoport bármelyikének közvetlen leszámlálására. Ez azért is érdekes, mert

S

a 2. ábrán felsorolt hat, páronként közös elem nélküli halmaznak is egyesítése, így a keresett érték ezek elemszámának összegeként is kiadódik.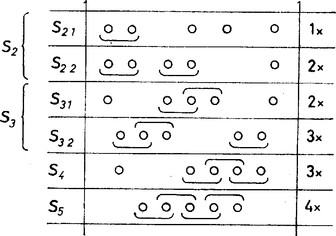

2. ábra

Vegyük észre, hogy a 2. ábra aszerint csoportosítja a számötösöket, hogy a kihúzott számokból álló "blokkok'' hány csoportra osztják a folyamatosan egymás mellé írt ki nem húzott számokat. Hogy szélről kihúzott számok esetén is valódi csoportokat kapjunk, vegyük a sor elejére a 0-t, a végére pedig a 91-et. Így a

87 = 92 - 5

darab ki nem húzott számot az első esetben 5, a másodikban és a harmadikban 4, a negyedikben és az ötödikben 3, a hatodikban pedig 2 összefüggő csoportra bontják a kihúzott számok.
Általában, ha

k

csoport jön létre, akkor 87 egyelőre számozatlan golyót sorba rakva a kihúzott számoknak megfelelő blokkok helyét a 87 golyó közti 86 hézag közül való alkalmas (

k - 1

)-nek a kijelölésével adhatjuk meg. Ebben a

k - 1

darab kiválasztott hézagban kell összesen 5 golyót elhelyeznünk úgy, hogy az egyes blokkok elemszáma a megadottakkal legyen egyenlő. Az összesen 92 golyó egy-egy elrendezésének az a számötös fog kölcsönösen egyértelműen megfelelni, amelyet a sorban álló golyók 0-tól 91-ig történő megszámozása után az utólag elhelyezett 5 golyó sorszámának leolvasásával kapunk. A kihúzott ‐ illetve beillesztett ‐ blokkok elemszám szerinti lehetséges sorrendjeit a

k - 1

hézagban számításba véve, az összes esetet megkapjuk.
A fentiek szerint

S_{22}

esetén az 1 hosszúságú " blokk'' a 86 közül kiválasztott 3 hézag bármelyikébe kerülhet, így

| S_{22} | = 3 \cdot (\binom{86}{3})

és hasonlóan

| S_{32} | = 2 \cdot (\binom{86}{2})

.
Innen

| S_{2} | = 8 801 240

, azaz

| S | = | S_{2} | + | S_{3} | + | S_{4} | + | S_{5} | = 9 122 966

. A keresett valószínűség így

| S | / (\binom{90}{5}) \approx 0, 2075

Megjegyzés. A fentiek szerint

S

-nek a 2. ábra szerinti felbontásában a további részhalmazok elemszáma közvetlenül megkapható. Így

\begin{matrix} | S_{21} | = 4 \cdot (\binom{86}{4}), | S_{31} | = 3 \cdot (\binom{86}{3}), | S_{4} | = 2 \cdot (\binom{86}{2}), végül | S_{5} | = (\binom{86}{1}) \end{matrix}

adódik. Újólag összegezve kapjuk, hogy

\begin{matrix} | S | = 4 \cdot (\binom{86}{4}) + 6 \cdot (\binom{86}{3}) + 4 \cdot (\binom{86}{2}) + (\binom{86}{1}) = \\ = (\binom{4}{1}) \cdot (\binom{86}{4}) + (\binom{4}{2}) \cdot (\binom{86}{3}) + (\binom{4}{3}) \cdot (\binom{86}{2}) + (\binom{4}{4}) \cdot (\binom{86}{1}) . & (*) \end{matrix}

Vegyük észre, hogy ha a 90 szám közül valahogyan megjelölünk négy darabot, akkor a (

*

) egyenlőség jobb oldalán éppen azoknak az ötösöknek a száma áll, amelyek legalább egyet tartalmaznak a megadott négy közül. Ha ehhez még hozzávesszük az egy megjelöltet sem tartalmazó

(\binom{86}{5})

darab számötöst, akkor éppen a 90 közül kiválasztható számötösök számát,

(\binom{90}{5})

-öt kapjuk. Innen

\begin{matrix} | S | = (\binom{90}{5}) - (\binom{86}{5}) . \end{matrix}

(**)

Megjegyzésünket és az első megoldást azzal zárjuk, hogy

| S |

legutolsó kifejezésében a kivonandó,

(\binom{86}{5})

éppen az olyan felosztások száma, ahol 5 darab egy-egy hosszúságú kihúzott blokk osztja 5 részre a sorba rakott 87 golyót. Az ilyen felosztások révén nyert számötösök pedig éppen a nem

S

-beliek, tehát azok, amelyek egyetlen szomszédos párt sem tartalmaznak. Így viszont közvetlenül adódik a (

* *

) összefüggés, és ezzel eljutottunk a megoldás legegyszerűbb alakjához: a kidolgozott leszámolási módszert egy speciális esetre alkalmazva azonnal megkapjuk a vizsgált

S

halmaz komplementerének elemszámát. A megoldás így a "hézagos'' leszámolási módszer ismertetésére és erre az utolsó bekezdésre rövidíthető.
A most következő megoldásból kiderül, hogy a komplementer halmaz közvetlenül is vizsgálható.

II. megoldás. Jelölje most

S^{*}

az első megoldásban szereplő

S

halmaz komplementerét, azaz azoknak a számötösöknek a halmazát, amelyekben nincsenek szomszédos számok. A keresett valószínűség ekkor nyilván

1 - | S^{*} | / (\binom{90}{5})

(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}) \in S^{*}

és az öt elem nagyság szerint növekvően van rendezve, akkor a

\begin{matrix} b_{1} = a_{1}, b_{2} = a_{2} - 1, b_{3} = a_{3} - 2, b_{4} = a_{4} - 3, b_{5} = a_{5} - 4 \end{matrix}

(1)

összefüggésekből kapott (

b_{1}, b_{2}, b_{3}, b_{4}, b_{5}

) számötös elemei különbözők, továbbá fennáll rájuk, hogy

\begin{matrix} 0 < b_{1} < b_{2} < b_{3} < b_{4} < b_{5} \leq 86. \end{matrix}

(2)

Megfordítva, minden olyan (

b_{1}, b_{2}, b_{3}, b_{4}, b_{5}

) számötöshöz, amelyre teljesül (2), az (1) szerint kiszámolt

a_{i}

értékek olyan 1 és 90 közti egészek, amelyek között nincsenek szomszédosak.
Ez azt jelenti, hogy az (1) alatti összefüggések kölcsönösen egyértelműen képezik le az

S^{*}

halmazt az első 86 pozitív egészből kiválasztható számötösök halmazára, a két halmaznak ezért ugyanannyi eleme van.

Így

(\binom{86}{5})

olyan lottóhúzás lehetséges, amikor a kihúzott számok között nincsenek szomszédosak. A keresett valószínűség ezután

1 - (\binom{86}{5}) / (\binom{90}{5}) \approx 0, 2075

Megjegyzés. Az eredmény szerint átlagosan minden ötödik húzásban várható együtt valamilyen szomszéd pár. A magyar lottóhúzások 1957-től 1986. augusztus végéig lefolyt 1585 húzása közül 323-ban fordult elő legalább egy szomszédosság. A

323 / 1585 = 0, 204

feltűnően közel áll a fent kapott valószínűséghez.
Ha viszont külön-külön nézzük meg, hogy hányszor került sor szomszédságra a növekvő felsorolás 1. és 2. helyén, 2. és 3. helyén stb. álló számok között, úgy már elég nagy eltéréseket látunk: 84, 66, 102 és 81. Ezek összege 333, ugyanis 10 esetben két szomszédosság is adódott, ebből 3 alkalommal

n

n + 1

n + 2

, típusú, tehát

S_{3}

-beli.
Még nagyobb szóródás mutatkozik, ha tovább bontjuk a fentieket az (1, 2), a (2, 3),

...

, és a (89, 90) közti szomszédságokra. Négy számpár csak egyszer fordult elő (pl. a 89 és a 90), 24 pár 2-szer, ezután rendre 17, 19, 12, 6, 4, 1, illetve 2 pár 3, 4,

...

, 9 esetben. (9-szer fordult elő a (33, 34) és a (66, 67) pár.) Egyáltalán, már az is figyelemre méltó, hogy mind a 89-féle szomszédság előfordult, az utolsó az 1397. húzáskor. Ugyanis az elgondolható

(\binom{90}{2}) = 4005

számpár közül 75 még egyáltalán nem fordult elő ‐ például az (1, 90) sem. Egy húzás

(\binom{5}{2}) = 10

számpárt tartalmaz és a 15 850 kihúzott számpár még nem adta ki a 4005 lehetségeset.
Ismét más érdekesség: a 902‐905. húzások mindegyike tartalmazott szomszédos számpárt, 7 más sorozatban 3-szor, 45 alkalommal pedig 2 egymás utáni húzásban került sor szomszédos számok kihúzására. Ezekkel szemben már volt 30 egymás utáni, szomszédság nélküli húzás is.