Feladat: Gy.2316 Korcsoport: 16-17 Nehézségi fok: nehéz
Füzet: 1986/november, 385 - 386. oldal  PDF  |  MathML 
Témakör(ök): Egyenes, Gördülés (Mozgási geometria), Gyakorlat
Hivatkozás(ok):Feladatok: 1986/január: Gy.2316

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy a k kis kör kerületének egy rögzített pontja a K nagy kör egy átmérőjét írja le.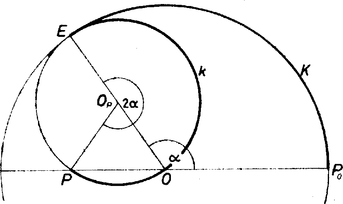
Jelöljük a K kör középpontját O-val! Mivel a k kör belülről érinti a K-t, ezért mozgás közben a k kör mindig áthalad az O ponton; továbbá a két kör érintkezési pontja, E rajta van a két kör középpontját összekötő egyenesen, a körök közös átmérőjén.
Tekintsük azt a helyzetet, amikor a mozgó k kör kerületének rögzített P pontja a K kerületén is rajta van! Jelöljük a K kerületének ezt a pontját P0-lal! Vizsgáljuk meg, hová kerül a P pont, ha a két kör E érintési pontja elmozdul a K kör kerületén. Jelöljük ekkor a mozgó k kör középpontjának helyzetét Op-vel.
A csúszásmentes gördülés miatt a K kör EP⌢0 íve ugyanolyan hosszú, mint a k kör EP⌢ íve. Tudjuk, hogy a körív hossza egyenesen arányos az ívhez tartozó középponti szöggel és a kör sugarával, tehát a két ív pontosan akkor egyenlő, ha a kis körben az EP ívhez kétszer akkora középponti szög tartozik, mint a nagy körben az EP0 ívhez.

 
 
1. ábra
 

Ezt felhasználva megmutatjuk, hogy a P pont mindig rajta van az OP0 egyenesen. A bizonyítást abban az esetben írjuk le, amikor a P0OE szög hegyesszög (1. ábra). Ugyanígy látható be az állítás akkor is, amikor a P0OE szög tompaszög (2. ábra), illetve homorúszög.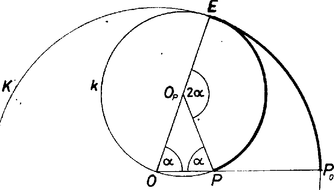
 
 
2. ábra
 

Legyen P0OE∢=α, ekkor POpE∢=2α. Az OpOP háromszögben OpO=OpP=r, tehát OpOP∢=OpPO∢=α, mert a háromszög Op csúcsánál lévő külső szöge 2α. Így OpOP∢=OpOP0∢, a PO és a P0O egyenlő szöget zárnak be a két kör közös átmérőjével, tehát a P pont rajta van az OP0 félegyenesen.
Megmutatjuk, hogy mozgása során a P pont az OP0 átmérő minden pontjába eljut. Legyen Q az átmérő egy tetszőleges pontja! Ha Q megegyezik O-val, akkor egy fél fordulat megtétele után a P éppen Q-ban van. Ha Q és O különbözők, akkor tekintsük az OQ felező merőlegesének és a mozgó kör középpontja pályájának, az O középpontú r sugarú körnek az egyik ‐ mindig létező ‐ közös pontját, ez legyen OQ. A kis körnek abban a helyzetében, amikor a középpontja OQ-ba kerül, a P pont nyilván éppen Q-val esik egybe.
Ezzel állításunkat teljes egészében beláttuk.
 

Megjegyzések. 1. A bizonyításból következik, hogy a k kör P-vel átellenes pontja a K kör OP0-ra merőleges átmérőjét írja le. A k körlemez tetszőleges pontját tekintve megmutatható, hogy a k mozgása során ellipszis alakú pályán mozog.
2. A feladat állításának műszaki alkalmazása nyilvánvaló: egy 2:1 arányú fogaskerék-rendszer a forgó mozgást egyenes vonalú ide-oda mozgássá alakítja át.