Kezdőlap


Feladat:	Gy.2298	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1986/május, 211 - 212. oldal		PDF \| MathML
Témakör(ök):	Középpontos tükrözés, Pont körüli forgatás, Mértani helyek, Terület, felszín, Négyzetek, Síkgeometriai számítások trigonometria nélkül négyszögekben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1985/november: Gy.2298

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen a négyzet oldala $a .$ Jelölje $M_{1}$ és $M_{2}$ a sík egy tetszőleges pontjából az $A C$ , illetve a $B D$ egyenesekre bocsátott merőlegesek talppontját, $m_{1}$ és $m_{2}$ pedig az $M M_{1}$ , illetve az $M M_{2}$ távolságot!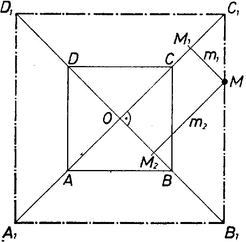

1. ábra

Ekkor a feltételek szerint az

M

pontosan akkor tartozik a keresett halmazhoz, ha

\begin{matrix} \frac{a \cdot \sqrt[]{2} \cdot m_{1}}{2} + \frac{a \cdot \sqrt[]{2} \cdot m_{2}}{2} = a^{2}, \end{matrix}

vagyis

\begin{matrix} m_{1} + m_{2} = a \cdot \sqrt[]{2} . \end{matrix}

Tehát a sík azon pontjait keressük, amelyeknek az

A C

és

B D

egyenesektől mért távolságaik összege

a \cdot \sqrt[]{2}

.
Az

A C

és

B D

egyenesek a síkot négy részre bontják; ezeket a részeket a két egyenes

O

metszéspontja körüli

90^{\circ}

-os forgatások egymásba viszik. Elegendő tehát a keresett halmaz pontjait az

O B

és

O C

félegyenesek által határolt síknegyedben meghatároznunk.
Legyen

M

ennek a síknegyednek egy tetszőleges pontja. Messe az

M

-en átmenő,

B C

-vel párhuzamos egyenes az

O B

és

O C

félegyeneseket a

B_{1}

, illetve

C_{1}

pontokban! Ekkor

M M_{1} = M_{1} C_{1}

és

M M_{2} = M_{1} O

, tehát

m_{1} + m_{2} = O C_{1}

. Az

M

pont tehát pontosan akkor tartozik a keresett halmazhoz, ha

O C_{1} = a \cdot \sqrt[]{2}

. Ámde

O C = \frac{a \cdot \sqrt[]{2}}{2}

miatt ez pontosan akkor igaz, ha

M

rajta van a

B C

szakasznak az

O

középpontból való,

2 : 1

arányú nagyítással keletkező képén. Tehát figyelembe véve az

O

körüli

90^{\circ}

-os elforgatásokat, a keresett halmaz az

A B C D

négyzet kerületének az

O

középpontból való

2 : 1

arányú nagyításával keletkező négyzet kerülete.

Megjegyzés. Ha az

M

pont a nagyított négyzet valamelyik csúcsa, akkor az

M A C

és

M B D

háromszögek egyike elfajul, területe

0

. Amennyiben ezt nem tekintjük háromszögnek, akkor a nagyított négyzet csúcsait a keresett halmazból ki kell zárni.

II. megoldás. Legyen

M

a sík egy tetszőleges pontja, és tükrözzük

M

-et a négyzet

O

középpontjára (

M \neq O

nyilván föltehető). Ha

M^{'}

jelöli a tükörképet, akkor az

M M^{'}

egyenesnek a négyzet négy oldalszakasza közül két szembenlevőn biztosan van pontja. Legyen ez a két oldal az

A B

és a

C D

. Ez azt jelenti, hogy

M

C O D

derékszögtartományok valamelyikében van (a határoló egyeneseket is beleértve).
A következőkben az idomok szokásos, csúcsaik körüljárásával való leírását egyszersmind a területük jelölésére is használjuk. Nem lesz félreérthető, hogy adott esetben a jel melyik értelmére kell gondolnunk. A tükrözés miatt

\begin{matrix} M A C = M M^{'} C és M B D = M M^{'} D . \end{matrix}

C O D

szögtartományban levő

M

pontok tehát akkor és csak akkor tartoznak a keresett halmazhoz, ha az

M D M' C

négyszög területe egyenlő a négyzet területével.
A keresett halmaznak így csak a négyzeten kívül lehetnek pontjai, hiszen belső vagy határpontokra az

M D M' C

négyszög valódi része a négyzetnek (2/a ábra).

2/a ábra

2/b ábra

M

‐ és így

M'

is ‐ külső pont, akkor a négyszög területe akkor és csak akkor lesz egyenlő a négyzet területével, ha

M

-nek és

M'

-nek a közös

D C

négyzetoldaltól mért távolságösszege ‐ mint az

M D C

és az

M' D C

háromszögek magasságainak összege ‐ éppen a négyzet oldalának kétszerese (2/b ábra).
A szimmetria miatt e két magasság összege éppen az

M

-nek a

D C

-től (vagy

A B

-től) mért távolsága kétszeresével nagyobb a négyzet oldalánál. Így

M

akkor és csak akkor tartozik a keresett halmaz

C O D

szögtartománybeli részéhez, ha a

D C

-től (vagy

A B

-től) mért távolsága a négyzet oldalának a felével egyenlő és

M

a négyzeten kívül helyezkedik el. Így éppen az első megoldásban kapott halmazt, pontosabban annak a

C O D

szögtartományokba eső részét kapjuk (3. ábra). Maga a keresett halmaz úgy áll elő, ha a fenti gondolatmenetet a

C O B

szögtartományra is elismételjük.

3. ábra