Kezdőlap


Feladat:	Gy.2294	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Keleti Tamás
Füzet:	1986/május, 205 - 207. oldal		PDF \| MathML
Témakör(ök):	Egyenletek grafikus megoldása, Egyenletek, Egészrész, törtrész függvények, Gyakorlat
Hivatkozás(ok):	Feladatok: 1985/november: Gy.2294

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Készítsük el az $f (x) = {x}^{2}$ és a $g (x) = {x^{2}}$ függvények grafikonjának egy-egy részét. Az $f$ függvény periodikus, legkisebb periódusa 1, a görbe ágai pedig a normál parabola ívének eltoltjai (l. ábra).

1. ábra

g

grafikonját úgy kaphatjuk, hogy az

x

tengellyel párhuzamosan, egységenként haladva mintegy "fölszeleteljük" az

x \to x^{2}

függvény grafikonját és a félig nyílt görbedarabokat az

y

tengellyel párhuzamosan eltoljuk úgy, hogy kezdőpontjuk az

x

tengelyre essék (2. ábra).

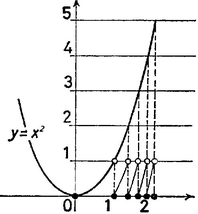2. ábra

Tekintsük most a két grafikont az

f

egy periódusán, a

[k, k + 1)

intervallumon, ahol

k ≧ 1

egész. Itt a

g

grafikonjának pontosan annyi ága halad, ahány egész szám van az

x \to x^{2}

értékkészletében, ha

x

[k, k + 1)

intervallumon változik. Mivel ez a függvény szigorúan monoton növő, az ágak száma

{(k + 1)}^{2} - k^{2}

(3. ábra).

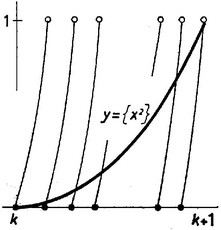3. ábra

Látható, hogy a legutolsó kivételével minden egyes ilyen ág metszi az

f

grafikonját, mégpedig pontosan egyszer. (A legelső ágnak éppen az

x

tengelyre eső kezdőpontja közös az

f

grafikonjával.) Ez azt jelenti, hogy az (1) egyenletnek

{(k + 1)}^{2} - k^{2} - 1

megoldása van a

[k, k + 1)

intervallumban.
Ennek megfelelően az

[k, k + 1)

intervallumban a gyökök száma

\begin{matrix} \sum_{k = 1}^{99}({(k + 1)}^{2}-k^{2}-1) . \end{matrix}

Az összegben a négyzetszámok az első és az utolsó kivételével váltakozó előjellel kétszer szerepelnek, így a fenti összeg

100^{2} - 1^{2} - 99 = 9900

. Mivel ezeken kívül még

x = 100

is megoldás, így az egyenletnek 9901 megoldása van az

[1, 100]

intervallumban.

Megjegyzés. A fenti megoldásban ezt írtuk: "látható, hogy'' a

g

grafikonjának ágai egy pontban metszik az

f

grafikonját. Nos, valóban tettünk engedményeket a szemléletesség érdekében, de a grafikonokat az

x \to x^{2}

függvény képéből származtattuk, amelynek tulajdonságai jól ismertek. Amit a megoldásból ezután hiányolhatunk, az az, hogy nem mondtuk ki pontosan, hogy melyek azok a tulajdonságai a másodfokú függvénynek, amelyekre valóban hivatkoznunk kell.

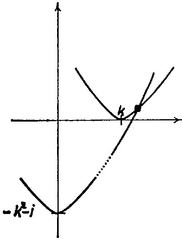4. ábra

Nos, áganként legalább egy közös pont létezése valóban nyilvánvaló, és az, hogy több nincsen, következik abból, hogy mindkét görberészlet parabolává egészíthető ki, amelyek az

x \to x^{2}

grafikonjának eltoltjai; egyikük az

x

, másikuk pedig az

y

tengellyel párhuzamosan (4. ábra). Ha pedig két egy állású egybevágó parabolának egynél több közös pontja van, akkor a két görbe azonos.
Aki még ezt az egy, a metszéspont létezését megerősítő ,,nyilvánvaló''-t is sokallja ‐ igaza van ‐, annak számára felírjuk azt az egyenletet, amely a kiegészített parabolák metszéspontjának

x

koordinátájára teljesül.
Az

f

grafikonjának

k

-adik íve az

y = {(x - k)}^{2}

, a

g

grafikonjának a

[k, k + 1)

intervallumbeli

i

-edik íve pedig az

y = x^{2} - (k^{2} + i)

egyenletű parabolává egészíthető ki. A görbék metszés pontjának

x

koordinátájára így

{(x - k)}^{2} = x^{2} - (k^{2} + i)

, azaz

x = k + \frac{i}{2 k}

teljesül,

i = 0, 1, ..., 2 k

.
Ezek a gyökök a legutolsó kivételével valóban a

[k, k + 1)

intervallumba esnek, így az eredeti egyenletnek pontosan

2 k

, azaz

({(k + 1)}^{2} - k^{2} - 1)

megoldása van a

[k, k + 1)

intervallumban. Ezzel az (1) megoldásait is megkaptuk, bár ez nem volt feladatunk.

II. megoldás. Legyen most is

k ≧ 1

egész, és vizsgáljuk (1) megoldásait a

[k, k + 1)

intervallumban. Ha

k ≦ x < k + 1

, akkor legyen

x = k + α

; ekkor nyilván

α = {x}

. Behelyettesítve (1)-be kapjuk, hogy

\begin{matrix} α^{2} = {{(k + α)}^{2}} = {k^{2} + 2 k α + α^{2}} . \end{matrix}

(2)

Itt a bal oldalon

0 ≦ α^{2} < 1

miatt

α^{2} = {α^{2}}

. Mármost két szám törtrésze pontosan akkor egyenlő, ha a két szám különbsége egész. Így kapjuk, hogy

(k^{2} + 2 k α + α^{2}) - α^{2} = k^{2} + 2 k α

egész, azaz

k

egész volta miatt

2 k α

is egész. Ha tehát

k ≧ 1

, akkor

k + α

pontosan azokra a

0 ≦ α < 1

számokra lesz (1) megoldása, amelyekre

2 k α

egész szám. Mivel ilyen egész szám pontosan

2 k

darab van, a

0, 1, 2, ..., 2 k - 1

, ezért az egyenletnek pontosan

2 k

megoldása van a

[k, k + 1)

intervallumban.
Így (1)-nek összesen

1 + \sum_{k = 1}^{99} 2 k = 9901

gyöke van az

[1, 100]

intervallumban (hisz

x = 100

is megoldás).

Megjegyzés. Az (1) egyenletnek az

[1; N]

intervallumban nyilván

N^{2} - N + 1

gyöke van, ha

N

egész. Ha pedig (1) helyett az

{x}^{n} = {x^{n}}

egyenlet megoldásainak a számát keressük, akkor az első megoldás gondolatmenetével kapjuk, hogy az

[1; N]

intervallumban a gyökök száma

\begin{matrix} 1 + \sum_{k = 1}^{N - 1} ({(k + 1)}^{n} - k^{n} - 1) = N^{n} - N + 1. \end{matrix}