Kezdőlap


Feladat:	Gy.2292	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Lovro Adrienn
Füzet:	1986/március, 119 - 120. oldal		PDF \| MathML
Témakör(ök):	Trigonometriai azonosságok, Szögfelező egyenes, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Gyakorlat
Hivatkozás(ok):	Feladatok: 1985/október: Gy.2292

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C$ háromszög oldalait a szokott módon rendre $a$ , $b$ , $c$ -vel! A $C$ csúcsból induló szögfelező és az $A B$ oldal metszéspontja legyen $F$ , az $F C$ szakasz hossza pedig $f$ . Legyen a $B C F ∢ = F C A ∢ = γ$ . A háromszög $T$ területét $a$ , $b$ és $f$ függvényében kell meghatároznunk.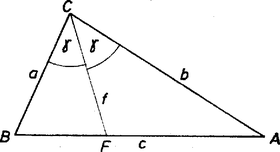

Ismert, hogy minden háromszög területének kétszerese megegyezik a háromszög két oldalának és az általuk bezárt szög szinuszának a szorzatával. Mivel az

A B C

háromszög területe az

A C F

és

F C B

háromszögek területének összege, ezért a fentiek szerint

\begin{matrix} a \cdot b \cdot sin 2 γ = b \cdot f \cdot sin γ + a \cdot f \cdot sin γ = (a + b) \cdot f \cdot sin γ . \end{matrix}

sin 2 γ = 2 sin γ \cdot cos γ

azonosság szerint innen

\begin{matrix} 2 \cdot a \cdot b \cdot sin γ \cdot cos γ = (a + b) \cdot f \cdot sin γ \end{matrix}

adódik. Mivel

2 γ

egy háromszög szöge, ezért

sin γ > 0

, tehát egyszerűsíthetünk vele.

\begin{matrix} 2 \cdot a \cdot b \cdot cos γ = (a + b) \cdot f, azaz cos γ = \frac{(a + b) \cdot f}{2 a b} . \end{matrix}

sin γ > 0

miatt

sin γ = \sqrt[]{1 - cos^{2} γ}

. Ha itt

cos γ

helyére beírjuk a kapott kifejezést, akkor kapjuk, hogy

\begin{matrix} sin γ = \sqrt[]{1 - \frac{{(a + b)}^{2} f^{2}}{4 a^{2} b^{2}}} . \end{matrix}

Vagyis az

A B C

háromszög területe

\begin{matrix} T = \frac{a \cdot b \cdot sin 2 γ}{2} = \frac{2 \cdot a \cdot b \cdot sin γ cos γ}{2} = \\ = \frac{(a + b) f}{4 a b} \sqrt[]{4 a^{2} b^{2} - {(a + b)}^{2} f^{2}} . \end{matrix}

Ez a képlet pedig éppen a kívánt adatokkal fejezi ki a háromszög területét.