Feladat: Gy.2282 Korcsoport: 16-17 Nehézségi fok: átlagos
Füzet: 1986/február, 72 - 73. oldal  PDF  |  MathML 
Témakör(ök): Egyenlő szárú háromszögek geometriája, Körülírt kör, Egyenes, Kör (és részhalmaza), mint mértani hely, Trapézok, Négyszögek geometriája, Síkbeli szimmetrikus alakzatok, Parabola, mint mértani hely, Gyakorlat
Hivatkozás(ok):Feladatok: 1985/szeptember: Gy.2282

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Egy húrnégyszögben a szemközti szögek összege 180∘, ugyanakkor ha a négyszög trapéz, akkor a szárakon is ennyi a szögek összege. A körbe írt trapézban tehát egyenlők az alapon fekvő szögek, így az ilyen trapéz tengelyesen szimmetrikus, a tengely az alapok közös felező merőlegese.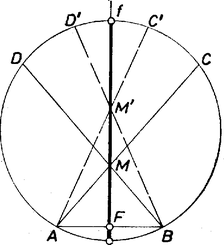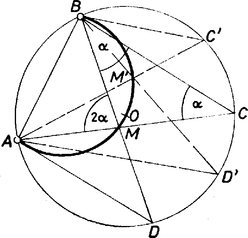
A megoldás során két esetet különböztetünk meg aszerint, hogy a betűzésből adódóan szomszédos A és B csúcsok a szóban forgó trapézok egy alapjának, vagy pedig egy szárának a végpontjai.
a) Legyen először AB a trapéz alapja. Ekkor a szimmetria miatt az átlók M metszéspontja rajta van az AB szakasz f felező merőlegesén, amely az ilyen trapézok szimmetriatengelye. A keresett pontok tehát az ABf felező merőlegesének a k kör belsejébe eső részén vannak.
Meg kell vizsgálnunk, hogy a fenti nyílt átmérőszakasz milyen M' pontjaihoz létezik olyan k-ba írt, AB oldalú trapéz, amelyben éppen M' az átlók metszéspontja. Nyilván ki kell zárnunk az f egyenesnek az AB szakasszal való metszéspontját, az AB szakasz felezőpontját. Az F-től különböző M' pontokra viszont az M'A és M'B egyenesek az f-re tükrös helyzetű C', illetve D' pontokban metszik a k kört, a kapott ABC'D' négyszög tehát a k körbe írt trapéz (1. ábra).
 
 
1. ábra
 

 
 
2. ábra
 

b) Tekintsük most azokat a k-ba írt trapézokat, amelyeknek AB az egyik szára. Jelöljük az AB húrhoz tartozó kerületi szöget α-val, az átlók metszéspontját pedig M-mel (2. ábra). Mivel BMC egyenlő szárú háromszög, a BMA külső szöge 2α. Az AB szakasz tehát állandó, 2α szögben látszik az M pontból, és ezért rajta van az AB szakasz 2α szögű látókörívének a k belsejébe eső ívén (ez egyébként az A, B, O pontokon átmenő kör, ahol O a k kör középpontja), hacsak 2α≠180∘, azaz az AB szakasz nem átmérője a k körnek. Ez utóbbi esetben nyilván nem létezik AB szárú k-ba írt trapéz.
Megfordítva, ha AB nem átmérő, akkor legyen M' a látókörív k belsejébe eső ívének tetszőleges pontja. Messe AM' és BM' a k kört C'-ben, illetve D'-ben. Ekkor AC'B∢=AD'B∢=α, másrészt az M'-nél létrejövő 2α külső szög miatt a D'BC' és a D'AC' szögek ugyancsak α-val egyenlők. BC' így párhuzamos AD'-vel, az ABC'D' négyszög tehát trapéz.
Összefoglalva, a keresett ponthalmaz az AB szakaszra merőleges átmérőnek a k belsejébe eső szakasza az F pont kivételével, továbbá ha AB nem átmérő, akkor az ABO háromszög körülírt körének a k kör belsejébe eső íve. (F az AB szakasz felező pontja, O pedig a k kör középpontja ‐ 3a, 3b ábrák.)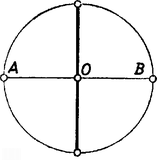
 
 
3.a ábra
 

 
 
3.b ábra