Kezdőlap


Feladat:	Gy.2278	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1986/március, 114 - 115. oldal		PDF \| MathML
Témakör(ök):	Gráfok összefüggősége, Fagráfok, erdők, faváz, Euler-gráfok (unikurzalitás), Síkbeli ponthalmazok távolsága, Gyakorlat
Hivatkozás(ok):	Feladatok: 1985/szeptember: Gy.2278

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A megoldás kulcsa az az észrevétel, hogy ha három adott város között fellépő három távolság közül kettőt ismerünk, akkor a harmadikat már ki tudjuk számolni. A városok ugyanis egy egyenes mentén helyezkednek el, így ez a harmadik távolság aszerint lesz a két ismert távolság összege vagy pedig a különbsége, hogy az a város, amelynek a másik kettőtől mért távolságát ismerjük, elválasztja-e a másik kettőt, vagy sem. Ezt felhasználva a megoldók módszeresen töltögették ki a hiányos táblázatot, míg végül valamennyi hiányzó értékre rátaláltak Az alábbiakból kiderül, hogy ez miért sikerülhetett.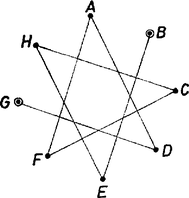
Áttekinthetőbb lesz a kép, ha az egyes városokat egy nyolcoldalú sokszög csúcsaiként ábrázoljuk és éllel kötjük össze azokat a csúcsokat, amelyeknek ismerjük a távolságát (1. ábra). Így egy úgynevezett gráfot kapunk.

1. ábra

Az ábrából látható, hogy a hét ismert útszakasz mentén a

B

városból indulva a

B E H C F A D G

útvonalon eljuthatunk a

G

városig úgy, hogy minden várost pontosan egyszer ejtünk útba. Igaz az is ‐ és ez a lényeg ‐, hogy bármely két város között létezik ismert hosszúságú szakaszokból álló útvonal, mégpedig csak egy. Kiszemelve most már egyet a városok közül ‐ legyen ez például az

A

‐, a további városok

A

-tól mért távolsága az

A

-ból hozzájuk vezető útvonal mentén haladva határozható meg az adott és az útközben megismert távolságok alapján a bevezetőben említettek szerint. Az

A

város esetében ez az

A D G

, illetve az

A F C H E B

útvonalak bejárását jelenti,
Az

A D G

útvonal mentén kapjuk, hogy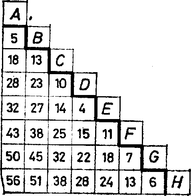

\begin{matrix} A D & = 28 adott, és \\ A G & = A D + D G = 28 + 22 = 50, \end{matrix}

A F C H E B

útvonalon pedig

\begin{matrix} A F & = 43 adott \\ A C & = A F - F C = 43 - 25 = 18, \\ A H & = A C + C H = 18 + 38 = 56, \\ A E & = A H - H E = 56 - 24 = 32, végül \\ A B & = A E - E B = 32 - 27 = 5. \end{matrix}

2. ábra

Miután pedig ismerjük egy városnak az összes többitől mért távolságát, bármely két város távolsága meghatározható. A teljesen kitöltött táblázatot a 2. ábra mutatja. A szomszédos városok közti távolságok:

A B = 5

B C = A C - A B = 13

C D = A D - A C = 10

D E = A E - A D = 4

E F = A F - A E = 11

F G = A G - A F = 7

G H = A H - A G = 6

Megjegyzés. Látható, hogy feladatunk az ismertnek adott távolságok bármely értéke mellett egyértelműen megoldható. Ez nyilván általában is igaz, ha az 1. ábra mintájára elkészített gráf összefüggő ‐ azaz bármely két pontja között vezet út és a gráf ún. ,,fa'' is ‐ azaz bármely két pontja között csak egy út vezet. Nem összefüggő gráfra a feladat nem oldható meg, ha pedig vannak olyan városok, amelyek között több út is vezet, akkor az ezek szakaszaira vonatkozó feltételek nem függetlenek, a feladatnak igy nincs mindig megoldása.
Mivel egy

n

pontú fának

n - 1

éle van, általában az mondhatjuk, hogy az összes távolságok meghatározásához

n - 1

távolság megadása szükséges és ennyi elegendő is, ha az ismert hosszúságú szakaszok egy fa éleit alkotják.