Kezdőlap


Feladat:	Gy.2268	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Molnár-S. Viktor , Tornyi Lajos
Füzet:	1986/április, 168 - 169. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Indirekt bizonyítási mód, Paralelogrammák, Húrnégyszögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1985/április: Gy.2268

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen az $A M$ egyenesnek a $k_{2}$ körrel alkotott másik metszéspontja $D$ . (A $D$ pont mindig létrejön, mert ha az $A M$ egyenes érintené a $k_{2}$ kört, akkor az $M$ pontot a $k_{2}$ kör $O_{2}$ középpontjával összekötő egyenes merőleges volna az $A M$ egyenesre, vagyis az $A B O_{2} M$ négyszög húrnégyszög lenne, tehát az $O_{2}$ pont rajta lenne a $k_{1}$ körvonalon. Ez viszont nyilván nem lehet. ‐ Az ábrán $D$ pótland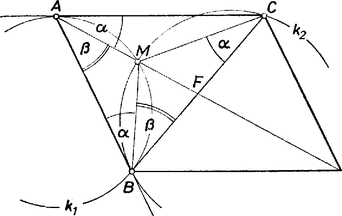ó.)

M A B ∢ = M B C ∢

, mint a

k_{1}

kör

M B

ívéhez tartozó kerületi, illetve érintő szárú kerületi szög.

M B C ∢ = M D C ∢

, mert mindkettő a

k_{2}

kör

M C

ívéhez tartozó kerületi szög. Tehát

\begin{matrix} D A B ∢ = M A B ∢ = M D C ∢ = A D C ∢, \end{matrix}

és így az

A B

egyenes párhuzamos a

C D

egyenessel.
Hasonlóan kapjuk, hogy

\begin{matrix} C A D ∢ = C A M ∢ = A B M ∢ = B D M ∢ = B D A ∢ . \end{matrix}

Ezért az

A C

egyenes párhuzamos a

B D

egyenessel.
Így az

A B D C

négyszög paralelogramma, ezért átlói felezik egymást, tehát az

A M

egyenes valóban áthalad a

B C

szakasz felezőpontján.

II. megoldás. Legyen

A B M ∢ = α

M A B ∢ = β

. Legyen az

F

pont az

A M

egyenesnek a

B C

egyenessel alkotott metszéspontja. A kerületi szögek tételének többszöri felhasználásával kapjuk, hogy

\begin{matrix} M A C ∢ = α, M C B ∢ = α, M B C ∢ = α . \end{matrix}

Ennek alapján a

B F M

és

A F B

háromszögek, továbbá a

C F M

és

A F C

háromszögek hasonlóak, mert szögeik egyenlőek. Ekkor viszont a megfelelő oldalak arányai is egyenlőek, azaz

\begin{matrix} \frac{B F}{F M} = \frac{A F}{F B}, ebből : {(B F)}^{2} = A F \cdot F M, illetve & (1) \\ \frac{C F}{F M} = \frac{A F}{F C}, azaz {(C F)}^{2} = A F \cdot F M . & (2) \end{matrix}

(1) és (2) egybevetéséből kapjuk, hogy

B F = C F

, vagyis az

F

pont valóban felezi a

B C

szakaszt.
Ezzel a bizonyítandó állítást beláttuk.