Kezdőlap


Feladat:	Gy.2236	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Pesti Péter
Füzet:	1985/szeptember, 256. oldal		PDF \| MathML
Témakör(ök):	Háromszögek egybevágósága, Húrnégyszögek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1984/december: Gy.2236

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az azonos íven nyugvó kerületi szögek egyenlősége miatt $C B D ∢ = C A D ∢$ és $B D C ∢ = B A C ∢$ . A $B C D$ háromszögben $B N C ∢ + D N C ∢ = 180^{\circ}$ , így a $B N C$ és $D N C$ háromszögek a $B N = N D$ oldaluk mentén összeillesztve egy háromszöget alkotnak (2.ábra).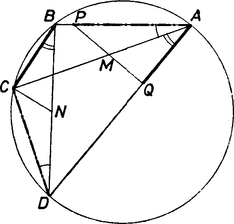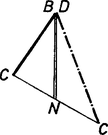

1. ábra

2. ábra

Az újonnan kapott háromszögben természetesen

N

oldalfelező pont, és a háromszög egybevágó az

A P Q

háromszöggel:

A P = C D

A Q = B C

és

P A Q ∢ = P A M ∢ + M A Q ∢ = C D N ∢ + N B C ∢

miatt. Az egybevágóságban az

N

pont megfelelője a

P Q

felezőpontja, vagyis az

M

pont lesz, így

M P = N C

. Ezt akartuk bizonyítani.

Megjegyzés. A bizonyításban nem használtuk fel, hogy

P

és

Q

A B

, illetve

A D

szakaszok belső pontja. Ha közülük valamelyik (vagy mindkettő) a körvonalra vagy azon kívül esik, az állítás akkor is igaz.