| Feladat: | Gy.2221 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Szabó Péter | ||
| Füzet: | 1985/április, 168 - 169. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Derékszögű háromszögek geometriája, Sokszög lefedések, Lefedések, Skatulyaelv, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1984/október: Gy.2221 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. A bizonyítás a következő ötleten alapszik. Osszuk fel a háromszöget 12 részre úgy, hogy a részek mindegyike lefedhető legyen egy 5/17 átmérőjű körrel. Ha mindegyik rész csak 2 pontot tartalmazna, akkor az elhelyezett pontok száma legfeljebb 24 lenne. Így a pontok tetszőleges elhelyezése esetén van olyan rész, ami legalább három pontot tartalmaz, kell tehát, hogy legyen a részeket lefedő körök között is egy, amelyik 3 pontot tartalmaz. 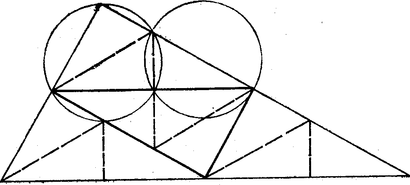 Először meghúztuk a derékszögű háromszög középvonalait. Így 4 egybevágó, 1/2 egység átfogójú derékszögű háromszöget kaptunk. Majd ezeket osztottuk tovább 3‐3 egybevágó derékszögű háromszögre úgy, hogy először meghúztuk a -os szög felezőjét, majd ennek talppontjából merőlegest állítottunk az átfogóra. A kapott 12 db háromszög egybevágó és átfogójuk Rajzoljuk meg a háromszögek körülírt köreit, ezek lefedik a háromszög valamennyi pontját, s így az elmondottak szerint kell, hogy legyen köztük egy, amelyik 3 pontot tartalmaz az adottak közül. 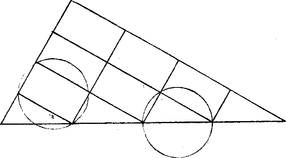 A 2. ábra a háromszög egy másik lehetséges felbontását mutatja. Ebben a háromszöget 10 részre bontottuk (6 egybevágó téglalapra és 4 egybevágó derékszögű háromszögre). Mindegyik rész lefedhető egy átmérőjű körrel. Eszerint már 21 pont között is van 3 olyan, amely lefedhető egy 5/17 átmérőjű körrel. Ennél a felosztásnál nem használtuk ki, hogy a derékszögű háromszög egyik szöge -os, csupán csak azt, hogy az átfogója egységnyi. |