| Feladat: | Gy.2204 | Korcsoport: 16-17 | Nehézségi fok: nehéz |
| Megoldó(k): | Benczúr András , Bíborka Judit , Csott Róbert , Deák CS. , Grallert Ágnes , Hetényi Zs. , Hornyák Z. , Jedlovszky P. , Kristóf Á. , Regős G. , Ribényi Á. , Rimányi R. , Szalay Gy. , Szkaliczky T. , Várkonyi V. | ||
| Füzet: | 1985/március, 116 - 119. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Számtani-mértani egyenlőtlenségek, Paralelogrammák, Szélsőérték-feladatok differenciálszámítás nélkül, Síkgeometriai szerkesztések, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1984/május: Gy.2204 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Feltehetjük, hogy a pontok a félkörön az , , , , sorrendben követik egymást. Megállapítjuk, hogy minden megengedett helyzetében és a szakasz belső vagy határpontjai (ha egybeesik -vel vagy -vel), és hogy e pontok sorrendje , , és . 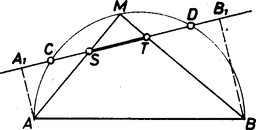 Vetítsük a egyenesre merőlegesen az és pontokat, a talppontok legyenek , illetve . Mivel , azért a szakasz -n túli meghosszabbításába esik, s hasonlóan ugyanennek a -n túli meghosszabbítására. Állítjuk, hogy az és szakaszok hosszának szorzata nem függ az pont helyzetétől. Valóban, és derékszögű háromszögek, és -nél, illetve -nél levő szögeik megegyeznek az -ben derékszögű háromszög egy-egy hegyesszögével. Így , azaz és hasonló háromszögek:
Eddig az szakasz hosszára kaptunk egy felső becslést: tudjuk, hogy ez helyzetétől függetlenül legfeljebb . Nekünk azonban ez nem elég: meg kell mutatni, hogy -nek van olyan helyzete, amelyhez tartozó szakasz hossza éppen ez az érték, és végül meg is kell szerkesztenünk az összes ilyen pontot. 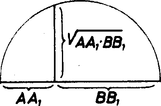 Ez utóbbi feladat az egyszerűbb. Láttuk, hogy csak akkor érheti el az (1)-beli felső határt, ha Az szakaszokat ismerjük, így mértani közepüket könnyen szerkeszthetjük például a magasságtétel segítségével (2. ábra). A szakaszt -től felé, valamint -től felé felmérve kapjuk az , pontokat; az és egyenesek metszéspontja adja ki -t (3. ábra). Ha tehát van a körívnek egyáltalán olyan pontja, amire az (1) szerinti maximális értéket felveszi, csak ez az pont lehet. 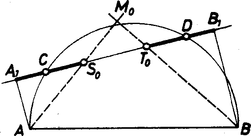 A feladat megoldásához így elegendő megmutatnunk, hogy az így megszerkesztett valóban pontja a körívnek ‐ ami egyúttal azt is adja, hogy az (1) szerinti maximumot az szakasz fel is veszi, és egyedül az pontban. Ez utóbbi állítás igazolását azzal kezdjük, hogy megmutatjuk: az , pontok , , , sorrendben helyezkednek el az egyenesen. Ehhez elegendő látni, hogy A íven tetszőleges pontot felvéve a hozzá tartozó , pontokra , így Az és egyenesek tehát metszik egymást, mégpedig az egyenesnek -val, -vel ellentétes partján. Így abból, hogy már következik, hogy a körív pontja. Először is, és hasonló derékszögű háromszögek, hiszen . Így Megjegyzés. A feladatnak megoldásánál alapvető fontosságú az a gyakran "elfelejtett'' rész, hogy a szerkesztés helyességét is igazolni kell. Abból ugyanis, hogy az szakasz hosszára (1)-ben egy felső korlátot találtunk, és megmondjuk, hogyan szerkesszük meg azt a pontot, amire ezt fel tudja venni, még nem következik, hogy a feladatot megoldottuk: mi biztosítja, hogy szerkesztésünk valóban ad pontot, és ráadásul az a ívre is esik? Azt hogy valóban ez a helyzet, külön igazolnunk kell, jelen esetben ez egyáltalán nem nyilvánvaló! II. megoldás. Húzzunk -n keresztül párhuzamost -vel, messe ez a félkört másodszor -ben (4. ábra). Tekintsük az egyenesnek azt a pontját, amelyre az négyszög paralelogramma. 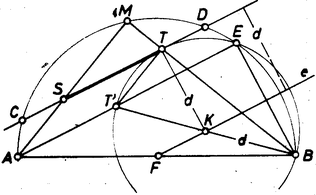 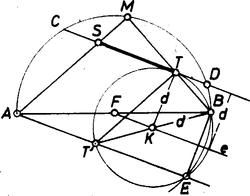 Mivel , , ezért belső pontja az szakasznak. Az derékszög, tehát és így annál nagyobb, minél rövidebb . Mivel és párhuzamos, . Legyen felezőpontja , erre Ha párhuzamost húzunk az átmérő felezőpontján át -vel, rajta lesz ezen az egyenesen, és nem kisebb, mint és az egyenes távolsága. Ha tehát tudunk olyan pontot szerkeszteni, amelyhez tartozó pontra akkor erre az pontra lesz az szakasz maximális. Ennek szerkesztése a következőképp történhet. középpontú, sugarú kört húzunk, ez az szakaszt pontosan egyszer metszi. Ugyanis az és távolságának kétszerese, ami kisebb és távolságának kétszeresénél, -nél, következésképp a körnek van metszéspontja az egyenessel. Másrészt kisebb a kör átmérőjénél, , így a kör és az egyenes egyik metszéspontja az szakaszon van, a másik a szakasz -n túli meghosszabbításán. Legyen ez a metszéspont . A mint átmérő fölé rajzolt kör éppen érinti a egyenest, hiszen középpontja távolságra van a egyenestől, és ennek a körnek a sugara. Legyen az érintési pont . Messe egyenes az fölötti félkört másodszor -ben. és a két szög egy szára közös, tehát és párhuzamos. Ebből következik, hogy csak a köríven és csak a szakaszon lehet. Állítjuk, hogy éppen a keresett pont, ami most már nyilvánvaló: és metszéspontját -sel jelölve a szerkesztett négyszög paralelogramma, tehát -hez éppen olyan tartozik, amelyre |