Kezdőlap


Feladat:	Gy.2188	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bíborka Judit
Füzet:	1985/február, 63 - 64. oldal		PDF \| MathML
Témakör(ök):	Geometriai egyenlőtlenségek, Trigonometriai azonosságok, Szögfelező egyenes, Gyakorlat
Hivatkozás(ok):	Feladatok: 1984/március: Gy.2188

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög szögeit a szokásos módon $α$ , $β$ , $γ$ -val, az $A$ -ból induló $f_{a}$ szögfelező és a $B C$ oldal metszéspontját $M$ -mel. ( $M$ nyilván belső pontja a $B C$ oldalnak.) Írjuk fel a $B A C$ , $B A M$ , $M A C$ háromszögek területét két oldaluk és a közbezárt szögnek a felhasználásával:

\begin{matrix} \frac{b c sin α}{2} = T_{B A C} = T_{B A M} + T_{M A C} = \frac{b f_{a} sin \frac{α}{2}}{2} + \frac{c f_{a} sin \frac{α}{2}}{2} . \end{matrix}

sin α = 2 sin \frac{α}{2} cos \frac{α}{2}

helyettesítéssel rendezés után kapjuk, hogy

\begin{matrix} \frac{cos \frac{α}{2}}{f_{a}} = \frac{1}{2 b} + \frac{1}{2 c} . \end{matrix}

Mivel

α

egy háromszög szöge,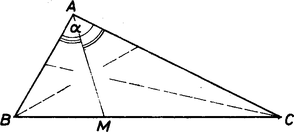

0^{\circ} < \frac{α}{2} < 90^{\circ}

, és ezért

0 < cos \frac{α}{2} < 1

, amiből

\begin{matrix} \frac{1}{2 b} + \frac{1}{2 c} = \frac{cos \frac{α}{2}}{f_{a}} < \frac{1}{f_{a}} . \end{matrix}

Hasonlóan adódik, hogy

\begin{matrix} \frac{1}{2 c} + \frac{1}{2 a} < \frac{1}{f_{b}}, és \frac{1}{2 a} + \frac{1}{2 b} < \frac{1}{f_{c}} . \end{matrix}

Az egyenlőtlenségek megfelelő oldalait összeadva

\begin{matrix} \frac{1}{a} + \frac{1}{b} + \frac{1}{c} < \frac{1}{f_{a}} + \frac{1}{f_{b}} + \frac{1}{f_{c}}, \end{matrix}

az állítás tehát valóban igaz.

Megjegyzés. Az is igazolható, hogy

\begin{matrix} \frac{1}{a} + \frac{1}{b} + \frac{1}{c} \leq \frac{2 \sqrt[]{3}}{3} (\frac{1}{f_{a}} + \frac{1}{f_{b}} + \frac{1}{f_{c}}), \end{matrix}

és egyenlőség csak a szabályos háromszögnél lép fel.