Kezdőlap


Feladat:	Gy.2170	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1985/március, 114 - 115. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Négyzetek, Gyakorlat
Hivatkozás(ok):	Feladatok: 1984/január: Gy.2170

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a négyzet oldala egységnyi, az egyik kör $k_{1}$ , és érintse ez $k_{2}$ -t és $k_{3}$ -at. Ekkor $k_{2}$ érinti $k_{1}$ -et, és $k_{3}$ és $k_{4}$ közül még egyet. Ez nem lehet $k_{3}$ , mivel ekkor $k_{1}, k_{2}$ és $k_{3}$ páronként érintenék egymást, és $k_{4}$ bármelyiket is érintené $k_{1}$ , $k_{2}$ , $k_{3}$ közül, az a többi körök közül hármat (és nem kettőt) érintene. Így $k_{2}$ csak $k_{1}$ -et és $k_{4}$ -et érintheti. Hasonlóan látható, hogy $k_{4}$ a $k_{2}$ -n kívül csak $k_{3}$ -at érintheti, s $k_{3}$ csak $k_{1}$ -et és $k_{4}$ -et. A feltétel szerint az érintő körök sugarai egyenlők, azért $k_{1}$ és $k_{4}$ sugara egyenlő ‐ mondjuk $r$ , továbbá $k_{2}$ és $k_{3}$ sugara is egyenlő ‐ $R$ .
Semelyik kör nem érintheti a négyzet szemben fekvő oldalait, hiszen a négyzetbe még egy ugyanakkora sugarú körnek el kell férnie. Így a körök két-két szomszédos oldalt érintenek, középpontjaik a négyzet átlóin helyezkednek el. Az is világos, hogy egyik sem érintheti belülről a másikat, tehát a négy kör a négyzet négy sarkában "ül''.
Tegyük fel először, hogy az $r$ sugarú $k_{1}$ és $k_{4}$ a négyzet szomszédos sarkaiban van. Mivel $k_{1}$ és $k_{4}$ nem metszheti egymást, sőt nem is érintheti, $r$ kisebb, mint a négyzet oldalának negyede, azaz 1/4. Hasonlóan $k_{2}$ és $k_{3}$ sugara is kisebb 1/4-nél, ekkor viszont $k_{1}$ és $k_{2}$ nem érinthetné egymást.

1. ábra

Ezért

k_{1}

és

k_{4}

, valamint

k_{2}

és

k_{3}

is a négyzet átellenes sarkaiban van (1. ábra).

k_{1}

sugara legfeljebb akkora lehet, hogy

k_{1}

és

k_{4}

metszés- és érintéspont nélkül elférjenek, vagyis hogy a

k_{1}

által az átlóból kivágott szakasz az átló felénél rövidebb legyen:

\begin{matrix} r \sqrt[]{2} + r < \frac{\sqrt[]{2}}{2}, \end{matrix}

azaz

\begin{matrix} r < \frac{\sqrt[]{2}}{2 (\sqrt[]{2} + 1)} = 1 - \frac{\sqrt[]{2}}{2} = 0, 2929. \end{matrix}

r

-et éppen (

1 - \sqrt[]{2} / 2

)-nek választjuk,

k_{1}

és

k_{4}

éppen érinti egymást a négyzet középpontjában. Ezekhez találhatók megfelelő

k_{2}

és

k_{3}

körök (2. ábra).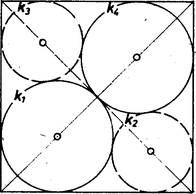

2. ábra

Ha most

k_{1}

(és

k_{4}

) sugarát folyamatosan csökkentjük, a hozzájuk tartozó

k_{2}

k_{3}

körök sugara folyamatosan nő.

r = 1 / 4

esetben mind a négy kör sugara egyenlő (3. ábra),

r

-et tovább csökkentve

k_{2}

és

k_{3}

növekszik, s

r

-et addig tudjuk csökkenteni, míg

k_{2}

és

k_{3}

"össze nem ér'' a négyzet középpontjában (4. ábra).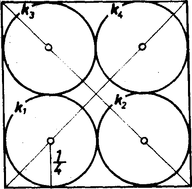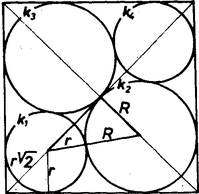

3. ábra

4. ábra

Ebben a helyzetben

k_{2}

és

k_{3}

sugara az előbb kiszámított

R = 1 - \sqrt[]{2} / 2

, s a vastagon kihúzott derékszögű háromszögből

\begin{matrix} {(r + R)}^{2} = R^{2} + {(\frac{\sqrt[]{2}}{2} - r \sqrt[]{2})}^{2}, \end{matrix}

azaz

\begin{matrix} r^{2} - 2 r (1 + R) + \frac{1}{2} = 0. \end{matrix}

Innen figyelembe véve, hogy

r < 1

, kapjuk, hogy

\begin{matrix} r = 2 - \frac{\sqrt[]{2}}{2} - \sqrt[]{4 - 2 \sqrt[]{2}} = 0,2105. \end{matrix}

k_{1}

kör sugara csak ennél nagyobb, és (

1 - \sqrt[]{2} / 2

)-nél kisebb lehet, ám ezek között tetszőleges értéket felvehet. A

k_{2}

és

k_{3}

körökre nyilván ugyanez a helyzet. Így a feladat kérdésére a válasz: a kérdéses körök sugarai az

\begin{matrix} (1 - \frac{\sqrt[]{2}}{2}, 2 - \frac{\sqrt[]{2}}{2} - \sqrt[]{4 - 2 \sqrt[]{2}}) \end{matrix}

nyílt intervallum valamelyik elemével, és csak ezekkel lehetnek egyenlők.