Kezdőlap


Feladat:	Gy.2165	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1984/szeptember, 254 - 255. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Gyakorlat, Térgeometriai bizonyítások, Mértani középtételek derékszögű háromszögekben
Hivatkozás(ok):	Feladatok: 1983/december: Gy.2165

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelölje $M$ az $A$ csúcsból a $P Q$ -ra bocsátott merőleges talppontját. Az $A R$ egyenes, a kocka éle, merőleges az $A P Q$ alapsíkra, így merőleges a sík valamennyi egyenesére, azaz $P Q$ -ra 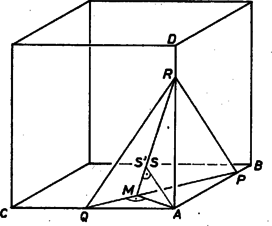is.

Legyen

S'

A

-ból az

M R

-re bocsátott merőleges talppontja. Belátjuk, hogy

S' \equiv S

, azaz

S'

megegyezik az

A

csúcsnak a

P Q R

síkra eső merőleges vetületével.

A S'

benne van az

A M R

síkban, melynek két egyeneséről:

A R

-ről és

A M

-ről tudjuk, hogy merőleges a

P Q

-ra. Akkor az

A M R

sík is merőleges a

P Q

-ra, ami azt jelenti, hogy a sík minden egyenese, így

A S'

is merőleges

P Q

-ra. Az

A S'

M R

-re is merőleges, amiből következik, hogy

A S'

merőleges a

P Q R

síkra. Az

A

csúcsból csak egy merőleges állítható a

P Q R

síkra és így valóban

S' \equiv S

.
Eszerint a

P Q S, P Q R

és

P Q A

háromszögek területei rendre

\begin{matrix} T_{1} = \frac{1}{2} P Q \cdot S M, T_{2} = \frac{1}{2} P Q \cdot R M és T_{3} = \frac{1}{2} P Q \cdot M A . \end{matrix}

Azt kell igazolnunk, hogy

T_{3} = \sqrt[]{T_{1} \cdot T_{2}}

, azaz

M A = \sqrt[]{S M \cdot R M}

. Ám az

A M S

és

R M A

derékszögű háromszögek hasonlók és ezért a befogó tétel szerint

\begin{matrix} M S \cdot M R = M A^{2}, \end{matrix}

amit bizonyítani akartunk.