Feladat: Gy.2163 Korcsoport: 16-17 Nehézségi fok: nehéz
Megoldó(k):  Bálint Katalin ,  Benczúr A. ,  Bíborka Judit ,  Burgmann L. ,  Dinnyés Enikő ,  Dobos S. ,  Domokos M. ,  Hajdú S. ,  Hornyák Z. ,  Jedlovszky P. ,  Klug R. ,  Kós G. ,  Kovács 968 Zs. ,  Kristóf Á. ,  Kunszt P. ,  Lipták 182 L. ,  Olasz Szabó M. ,  Papp 710 Zs. ,  Regős G. ,  Ribényi Ákos ,  Román L. ,  Sáhi A. ,  Schöffer Timea ,  Szigeti Z. ,  Szíjártó Katalin ,  Vindics P. 
Füzet: 1984/november, 382 - 383. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek egybevágósága, Síkgeometriai számítások trigonometria nélkül háromszögekben, Gyakorlat, Síkgeometriai bizonyítások, Középponti és kerületi szögek
Hivatkozás(ok):Feladatok: 1983/december: Gy.2163

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az AB szakasz felezőpontját F-fel, az AP és BP felezőpontját pedig G-vel, H-val. Az FGH háromszög a PBA középháromszöge, ezért GFHP paralelogramma ‐ speciálisan 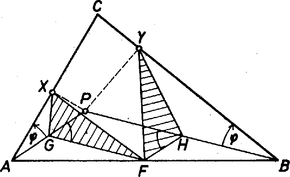PH=GP, GP=HF és PHF∢=PGF∢.

 
 

A P belső pontja az ABC háromszögnek, ezért a PAC∢=PBC∢=φ szög kisebb a háromszög A-nál és B-nél levő szögeinél, tehát φ mindenképpen hegyesszög. P-t az AC, BC egyenesekre vetítve az X, Y talppontok tehát az AC, illetve BC félegyenesekre esnek. Így az APX, BPY hasonló derékszögű háromszögek ellentétes körüljárásúak, és körülírt köreik középpontja G, illetve H.
Nézzük most az XGF, illetve YHF háromszögeket. Először is GX=GP, hiszen G az APX körülírt körének középpontja, és így előbbi megállapításunk szerint GX=GP=HF. Hasonlóan adódik, hogy HY=HP=GF, vagyis XGF és YHF két-két oldalban megegyezik. Megmutatjuk, hogy a közbezárt XGF∢ és YHF∢ szögek is egyenlők. Az XGP∢ az APX háromszög köré írt körben az XP húrhoz tartozó középponti szög, így kétszerese az ugyanehhez a húrhoz tartozó XAP∢ kerületi szögnek. Így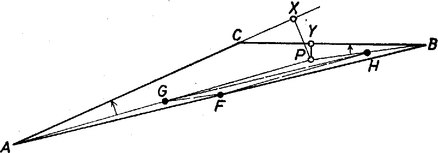
XGF∢=XGP∢+PGF∢=2⋅XAP∢+PGF∢=2⋅YBP∢+PHF∢,
hiszen a feltétel szerint XAP∢=YBP∢, és láttuk, hogy GFHP paralelogramma. Hasonlóan H a BPY derékszögű háromszög körülírt körének középpontja, így
2⋅YBP∢+PHF∢=YHP∢+PHF∢=YHF∢,
tehát XGF∢=YHF∢, ahogyan állítottuk. Ezért az XGF és YHF háromszögek egybevágók, G-vel, H-val szemközti oldaluk egyenlő: FX=FY.
 
 

Az F pont tehát egyenlő távolságra van X-től és Y-tól, így rajta van az XY szakasz felező merőlegesén.
Összefoglalva, az AB szakasz F felezőpontja a P minden megengedett helyzetében rajta van az XY felező merőlegesén, ezért a merőlegesek valóban egy ponton mennek át.