Kezdőlap


Feladat:	Gy.2162	Korcsoport: 14-15	Nehézségi fok: átlagos
Füzet:	1984/május, 216. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Húrsokszögek, Gyakorlat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1983/december: Gy.2162

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a hatszög csúcsai pozitív körüljárási irányban $A_{1} A_{2} A_{3} B_{1} B_{2} B_{3}$ . Ekkor $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ a kör átmérői, és a másodszomszédos csúcsok által meghatározott háromszögek az $A_{1} A_{3} B_{2}$ , ill. $B_{1} B_{3} A_{2}$ . Nyilván elegendő az állítást az egyik, pl. az $A_{1} A_{3} B_{2}$ háromszögre igazolni.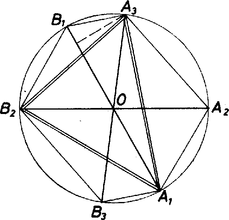

Legyen a kör középpontja

O

, ez belső pontja az

A_{1} A_{3} B_{2}

háromszögnek, s így területe egyenlő az

O A_{1} A_{3}

O A_{1} B_{2}

és

O B_{2} A_{3}

háromszögek területének összegével.
Vegyük észre, hogy

\begin{matrix} T (O A_{1} A_{3}) = T (O A_{3} B_{1}) = T (O B_{3} A_{1}), \end{matrix}

hiszen például az

O A_{1} A_{3}

háromszögben és az

O A_{3} B_{1}

háromszögben az

A_{3}

-ból induló magasság megegyezik, az

A_{3}

-mal szemben fekvő oldalak pedig egyenlők:

O A_{1} - O B_{1}

. Ezért

\begin{matrix} T (O A_{1} A_{3}) = \frac{T (O A_{3} B_{1}) + T (O B_{3} A_{1})}{2} . \end{matrix}

Hasonlóan kapjuk, hogy

\begin{matrix} T (O A_{3} B_{2}) = \frac{T (O A_{2} A_{3}) + T (O B_{2} B_{3})}{2}, \\ T (O B_{2} A_{1}) = \frac{T (O B_{1} B_{2}) + T (O A_{1} A_{2})}{2} . \end{matrix}

Ezeket összeadva a bal oldalon az

A_{1} A_{3} B_{2}

háromszög területe, a jobb oldalon a hatszög területének a fele adódik. Ezzel az állítást igazoltuk.