Kezdőlap


Feladat:	Gy.2154	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Jamrik Ferenc
Füzet:	1984/április, 168. oldal		PDF \| MathML
Témakör(ök):	Középpontos és egyéb hasonlósági transzformációk, Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat, Mértani középtételek derékszögű háromszögekben, Középponti és kerületi szögek
Hivatkozás(ok):	Feladatok: 1983/november: Gy.2154

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tegyük fel, hogy $k_{1}$ a nagyobbik kör, ekkor a közös érintők és a körök középpontját összekötő egyenes (a centrális) $P$ metszéspontja a centrálison $O_{1}$ -nek ugyanarra az oldalára esik, mint $O_{2}$ (l. ábra). A $P_{1}$ és $P_{2}$ érintési pontok $M_{1}$ , $M_{2}$ vetülete ugyancsak az $O_{1} P$ szakaszra esik. $M_{1}$ vagy elválasztja $O_{1}$ -et és $O_{2}$ -t, és akkor a pontok sorrendje $O_{1}$ , $M_{1}$ , $O_{2}$ , $M_{2}$ , $P$ vagy nem, és akkor a sorrend 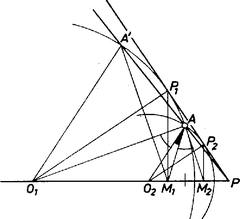$O_{1}$ , $O_{2}$ , $M_{1}$ , $M_{2}$ , $P$ .

A két kör metszéspontjának,

A

-nak a vetülete mindkét esetben az

M_{1}

és

M_{2}

közé esik. A bizonyítandó szögegyenlőség helyett az

O_{1} A M_{1} ∢ = O_{2} A M_{2} ∢

egyenlőséget fogjuk igazolni. Ez ekvivalens az eredeti egyenlőséggel, melyet az első esetben úgy kapunk, hogy az egyenlőség mindkét oldalából levonjuk a közös

O_{2} A M_{1} ∢

-t, a második esetben viszont a közös

O_{2} A M_{1}

szöget az egyenlőség mindkét oldalához hozzá kell adni.
Nagyítsuk ki a

k_{2}

kört

P

-ből mint középpontból úgy, hogy

k_{2}

-nek

k'_{2}

-vel jelölt képe

k_{1}

legyen. Ekkor

O_{2}

O_{1}

-gyel,

M'_{2}

M_{1}

-gyel,

P'_{2}

P_{1}

-gyel lesz azonos, az

A

pont képe

A'

P A

-nak

k_{1}

-gyel való második metszéspontja. A nagyítás szögtartó, ezért

O_{2} A M_{2} ∢ = O_{1} A' M_{1} ∢

. Az

O_{1} P_{1} P

derékszögű háromszögben

P_{1} M_{1}

magasság, a befogótételt alkalmazva

\begin{matrix} P P_{1}^{2} = P M_{1} \cdot P O_{1} . \end{matrix}

P

-ből mint külső pontból a körhöz húzott érintő és szelő szakaszra ismert mértani közép tétel szerint

\begin{matrix} P P_{1}^{2} = P A \cdot P A' . \end{matrix}

Amiből

P M_{1} \cdot P O_{1} = P A \cdot P A'

adódik, ami azt jelenti, hogy

M_{1}

O_{1}

és

A

A'

egy körön vannak, mégpedig vagy az

M_{1} O_{1} A A'

vagy pedig az

M_{1} O_{1} A' A

sorrendben. Az

O_{1} M_{1}

húrhoz tartozó kerületi szögekre

O_{1} A' M_{1} ∢ = O_{1} A M_{1} ∢

, és ezt akartuk igazolni.