Kezdőlap


Feladat:	Gy.2141	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Hajdu Sándor Zoltán
Füzet:	1984/március, 115 - 117. oldal		PDF \| MathML
Témakör(ök):	Gúlák, Szerkesztések a térben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1983/szeptember: Gy.2141

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a derékszögű háromszög csúcsait $A$ , $B$ , $C$ -vel, a gúla negyedik csúcsát $D$ -vel. Bocsássunk $D$ -ből merőlegest az $A B$ , $B C$ , $C A$ oldalakra és az alapsíkra, a talppontok rendre $E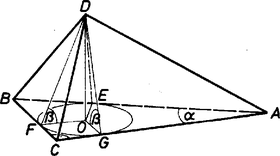$ , $F$ , $G$ és $O$ (1. ábra).

1. ábra

D O E

D O F

D O G

derékszögű háromszögekben az

E

-nél,

F

-nél,

G

-nél található hegyesszög az oldallapoknak az alapsíkkal bezárt szöge. Tudjuk ugyanis, hogy két sík hajlásszögét a metszésvonaluk egy pontjába a síkokon belül állított merőleges egyenesek szöge méri, és például

D E

és

O E

is merőleges

A B

-re (ez a "három egymásra merőleges egyenes'' néven ismert tételből adódik). Ezek a szögek tehát a feltétel alapján mind

β

-val egyenlők, továbbá a háromszögek

D O

befogója közös, következésképpen a

D O E

D O F

D O G

háromszögek egybevágók, és így

O E = O F = O G

. Az

O

pont tehát az

A B C

háromszög beírt körének középpontja.
Válasszunk az

A D

élen egy tetszőleges

P

pontot.

P

-ben állítsunk merőlegest

A D

-re az

A B D

és

A C D

síkokban, messék ezek az

A B

, ill.

A C

egyeneseket a

P_{1}

, ill.

P_{2}

pontokban. Az

A B D

és

A D C

síkok hajlásszöge definíció szerint a

P P_{1}

és

P P_{2}

félegyenesek szöge, azaz a

P P_{1} P_{2}

háromszög

P

csúcsánál levő szög.
Ezek után a szerkesztést a következőképpen végezhetjük el. Felveszünk a, gúla alapjához hasonló

A B C

derékszögű háromszöget. Ezt megtehetjük, hiszen az

A B C

háromszög egyik hegyesszöge,

α

, adott. Megszerkesztjük a beírt kör

O

középpontját és

O

-nak az oldalakra eső

E

F

G

vetületét (2. ábra).

2. ábra

D O E

derékszögű háromszögnek most már ismerjük az

O E

befogóját és a

D E O ∢ = β

szögét. A

D E = D F = D G

átfogó, mely egyúttal az oldallapok magasságvonala, könnyen szerkeszthető. Az oldallapokon a

D

-ből induló magasságvonalak talppontjai az

E

F

ill.

G

pontok, így az

A B D

és

A C D

oldallapok

A B D^{'}

és

A B D^{''}

leforgatottjait megszerkeszthetjük. Végül

A D

-n (melynek ábránkon két példánya szerepel) tetszőlegesen felvesszük a

P

pontot, azaz

A D^{'}

-n egy

P^{'}

és

A D^{''}

-n egy

P^{''}

pontot úgy, hogy

A P^{'} = A P^{''}

legyen. Az

A B D^{'}

háromszögben

P^{'}

-nél merőlegest állítunk

A D^{'}

-re, ez az

A B

oldalt

P_{1}

-ben metszi; az

A C D^{''}

háromszögben az

A D^{''}

-re

P^{''}

-ben emelt merőleges

A C

-t

P_{2}

-ben metszi. Végül vesszük azt a

P P_{1} P_{2}

háromszöget, melynek oldalai

P_{1} P_{2}

P^{'} P_{1}

és

P^{''} P_{2}

; ennek

P

-nél levő szöge az

A B D

és

A C D

lapok szöge.
A másik két oldallap hajlásszöge hasonlóan szerkeszthető.
Az

α

és

β

szögeknek hegyesszögeknek kell lenniük. Ezzel a megszorítással a kérdéses gúla létezik, és az (tükrözéstől és középpontos hasonlóságtól eltekintve) egyértelmű. Így a szerkesztést mindig végre lehet hajtani, és az ‐ könnyen ellenőrizhető módon ‐ helyes eredményt ad.

Megjegyzések. 1. A megoldásban nem használtuk ki, hogy a gúla alaplapja derékszögű háromszög, a szerkesztés tetszőleges alap esetén hasonlóan elvégezhető.
2. Belátható, hogy a

P P_{1} P_{2}

háromszög mindig egyenlő szárú. A

P

pont megfelelő megválasztásával elérhető, hogy a

P_{1}

pont

E

-vel, a

P_{2}

pedig

G

-vel essen egybe. Így a szerkesztést a következőképpen is be lehet fejezni. A

D^{'}

és

D^{''}

pontok szerkesztése után

E

-ből

A D^{'}

-re,

G

-ből

A D^{''}

-re állítunk merőlegest, a talppontok legyenek

P^{'}

, ill.

P^{''}

(3. ábra).

3. ábra

E

középpontú,

E P^{'}

sugarú és a

G

középpontú,

G P^{''} = E P^{'}

sugarú körök metszéspontja

P

. Az

A B D

és

A C D

lapok hajlásszöge megegyezik az

E P G

szöggel.