Kezdőlap


Feladat:	Gy.2140	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Ijjas Csaba
Füzet:	1984/március, 114 - 115. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Magasságpont, Trapézok, Gyakorlat, Síkgeometriai bizonyítások
Hivatkozás(ok):	Feladatok: 1983/szeptember: Gy.2140

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a trapéz csúcsait $A$ , $B$ , $C$ , $D$ -vel úgy, hogy $A B | | C D$ és $A B \geq C D$ . Az $A$ csúcs elhagyása után maradt $B C D$ háromszög magasságpontját jelölje $A^{'}$ , a $B$ elhagyásával kapott $A C D$ háromszög magasságpontját $B^{'}$ , és így tovább. Azt kell tehát igazolnunk, hogy $A^{'} B^{'} C^{'} D^{'}$ négyszög trapéz.
Először azt az esetet vizsgáljuk, mikor $A B > C D$ . Legyen az $A D, B C$ egyenesek metszéspontja $E$ . Az $A B E$ és $D C E$ háromszögek hasonlóak. Jelölje $M_{1}$ az $A D^{'}$ és $B C^{'}$ egyenesek metszéspontját, $M_{2}$ pedig a $C B^{'}$ és $D A^{'}$ egyenesekét, $A D^{'} ⊥ B E$ , valamint $B C^{'} ⊥ A E$ miatt $M_{1}$ az $A B E$ háromszög magasságpontja, hasonlóan $M_{2}$ a $C D E$ háromszög magasságpontja. Az $M_{1}$ , $M_{2}$ és $E$ pontok tehát egy egyenesen vannak és ez az egyenes merőleges $A B$ -re. Ugyancsak merőlegesek $A B$ -re az $A B^{'}$ , $C^{'} D$ , $C D^{'}$ és $A^{'} B$ egyenesek is, mert vagy egy $A B$ vagy egy $C D$ alapú háromszög magasságvonalai. Így ezek az egyenesek párhuzamosak egymással. Párhuzamosak egymással a $B M_{1}$ és $C M_{2}$ , valamint az $A M_{1}$ és $D M_{2}$ egyenesek: az első kettő az $A D$ , a második kettő pedig a $B C$ egyenesre merőleges (1. ábra).

Messe a

B M_{1}

magasságvonal az

A B^{'}

-t

C^{''}

-ben. Az

M_{1} M_{2} B^{'} C^{''}

négyszög szemben fekvő oldalai az előzőek alapján párhuzamosak egymással, ez a négyszög tehát paralelogramma. Hasonlóan kapjuk, hogy

M_{1} M_{2} A^{'} D^{''}

is paralelogramma, ahol

D^{''}

A M_{1}

, valamint

A^{'} B

metszéspontja. Következésképpen

B^{'} C^{''}

és

A^{'} D^{''}

párhuzamos és egymással egyenlő szakaszok (mindketten párhuzamosak és egyenlők

M_{1} M_{2}

-nel), tehát

A^{'} B^{'} C^{''} D^{''}

is paralelogramma ‐ speciálisan

A^{'} B^{'} | | C^{''} D^{''}

.
Tudjuk, hogy az

E M_{1}

D C^{'}

és

A C^{''}

egyenesek párhuzamosak. Így az

M_{1}

középpontú,

λ = \frac{E D}{E A}

arányú nagyításban

C^{'}

képe

C^{''}

lesz. Hasonlóan, az

M_{1}

középpontú,

λ^{'} = \frac{E C}{E B}

arányú nagyításban

D^{'}

képe

D^{''}

lesz. Az

A E B

és

D E C

háromszögek hasonlók, tehát

\begin{matrix} \frac{M_{1} C^{'}}{M_{1} C^{''}} = \frac{E D}{E A} = \frac{E C}{E B} = \frac{M_{1} D^{'}}{M_{1} D^{''}} . \end{matrix}

Az első és utolsó tagot összevetve láthatjuk, hogy azok éppen az

M_{1} C^{'} D^{'}

és

M_{1} C^{''} D^{''}

háromszögek hasonlóságát mondják ki, ezért

C^{'} D^{'} | | C^{''} D^{''}

.
Az előbb viszont láttuk, hogy

A^{'} B^{'} | | C^{''} D^{''}

, amiből következik, hogy

C^{'} D^{'} | | A^{'} B^{'}

, azaz a négyszög trapéz.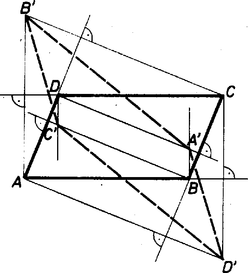

Végül ha

A B = C D

, akkor a trapéz paralelogramma (2. ábra). A paralelogramma középpontosan szimmetrikus az átlóinak metszéspontjára. Ebből következik, hogy az

A^{'}

B^{'}

C^{'}

D^{'}

magasságpontok ugyancsak szimmetrikusan helyezkednek el az átlók metszéspontjára, de akkor ezek is paralelogrammát határoznak meg. Ezzel az állítást igazoltuk.