| Feladat: | Gy.2138 | Korcsoport: 14-15 | Nehézségi fok: nehéz |
| Füzet: | 1984/március, 112. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Terület, felszín, Gyakorlat | ||
| Hivatkozás(ok): | Feladatok: 1983/szeptember: Gy.2138 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az elhelyezendő, sugarú kör középpontjára két feltételnek is kell teljesülnie. Az első, hogy legalább egység távolságra legyen a téglalap oldalaitól ‐ a körnek teljesen a téglalap belsejébe kell esnie. A második, hogy a kör középpontja minden kis négyzet oldaltól -nél nagyobb távolságra legyen, azért hogy ne legyen azokkal közös pontja. 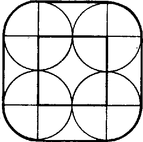 A második feltételt kielégítő pontokat először egy egységoldalú négyzetre keressük meg. Az egységoldalú négyzet pontjaitól legfeljebb egység távolságra levő pontok halmaza olyan alakzat, melyet egyrészt a négyzet oldalaival párhuzamos, egység távolságra haladó szakaszok, másrészt a csúcsok körül mint középpont körül írt sugarú negyedkörök határolnak. területét könnyen ki tudjuk számítani: |