Kezdőlap


Feladat:	Gy.2137	Korcsoport: 16-17	Nehézségi fok: átlagos
Füzet:	1984/február, 70 - 71. oldal		PDF \| MathML
Témakör(ök):	Egyéb sokszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1983/szeptember: Gy.2137

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha úgynevezett hurkolt sokszögeket is megengedünk, amelyekben az oldalak csúcsoktól különböző pontokban is metszik egymást ‐ akkor a feladat állítása nem igaz. Az 1. ábrán látható nyolcszög szögei $90^{\circ}$ -osak, oldalai pedig: 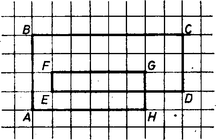$A B = 4$ , $B C = 8$ , $C D = 3$ , $D E = 7$ , $E F = 1$ , $F G = 5$ , $G H = 2$ , $H A = 6$ .

1. ábra

A feladat állítását azzal a pótlólagos feltétellel igazoljuk, hogy a sokszög konvex. Tegyük fel tehát, hogy létezik a feltételeknek eleget tevő nyolcszög. Az egyenlő szögeket jelölje

α

, az oldalakat pedig

a_{1}, a_{2}, ..., a_{8}

. Ismeretes, hogy egy konvex nyolcszög szögeinek összege

6 \cdot 180^{\circ} = 1080^{\circ}

, így

α = \frac{1080^{\circ}}{8} = 135^{\circ}

. Tehát a nyolcszög köré egy

A B C D

téglalap írható oly módon, hogy az

a_{1}

a_{3}

a_{5}

a_{7}

oldala a téglalap

A B

B C

C D

D A

oldalaira esnek (2. ábra).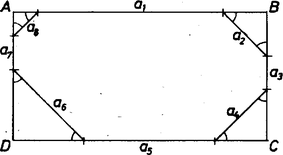

2. ábra

A téglalap

A B

és

C D

oldalát ‐ melyekről tudjuk, hogy egyenlő hosszúak ‐ a nyolcszög oldalaival kifejezve kapjuk, hogy

\begin{matrix} a_{1} + (a_{2} + a_{8}) \frac{\sqrt[]{2}}{2 |} = a_{5} + (a_{6} + a_{4}) \frac{\sqrt[]{2}}{2} . \end{matrix}

Ezt átrendezve adódik, hogy

\begin{matrix} \sqrt[]{2} = \frac{a_{6} + a_{4} - a_{2} - a_{8}}{a_{1} - a_{5}}, \end{matrix}

ahol a nevező nem 0, mert

a_{1}

és

a_{5}

feltétel szerint különbözők. Azt kaptuk, hogy

\sqrt[]{2}

előáll két egész szám hányadosaként, ami ellentmond

\sqrt[]{2}

irracionális voltának. Tehát valóban nem létezik a kérdéses nyolcszög.

Megjegyzések. 1. A fenti gondolatmenet ugyanúgy alkalmazható, ha az oldalakról csak azt tesszük fel, hogy hosszaik különböző racionális számok.
2. Az is könnyen belátható, hogy ha egy konvex nyolcszög szögei egyenlők és oldalai hossza racionális, akkor a párhuzamos oldalak egyenlő hosszúak.
3. Általában akkor és csak akkor létezik olyan konvex

n

-oldalú sokszög, melynek szögei egyenlők, oldalai pedig valamilyen sorrendben

1, 2, 3, ..., n

egységnyi hosszúak, ha

n

nem egy prímszám hatványa.