Kezdőlap


Feladat:	Gy.2130	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Bán Rita , Bangha Imre , Dringó L. , Edvi T. , Pintér A. , Simon Gy. , Werner P.
Füzet:	1983/december, 212 - 213. oldal		PDF \| MathML
Témakör(ök):	Síkgeometriai számítások trigonometria nélkül körökben, Gyakorlat
Hivatkozás(ok):	Feladatok: 1983/május: Gy.2130

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $E_{1}$ és $E_{2}$ a két párhuzamos érintőnek a $k_{1}$ körrel közös pontja. A feladat feltételeiből következik, hogy a további érintési pontok az $E_{1} E_{2}$ egyenesnek ugyanarra a partjára esnek. Jelölje a $k_{2}$ körnek és az $E_{1}$ -ben húzott érintőnek a közös pontját $E_{4}$ , $k_{3}$ és az $E_{2}$ -ben húzott érintő érintési pontját $E_{3}$ . Legyen továbbá $O_{i}$ a $k_{i}$ középpontja $(i = 1,2,3)$ ; $O_{2}$ -nek az $E_{1} E_{2}$ -re való merőleges vetülete 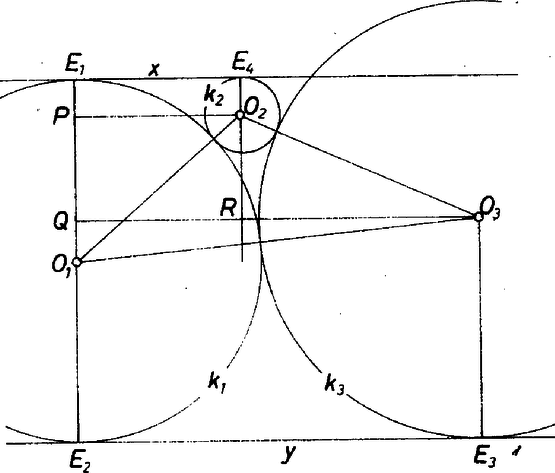$P, O_{3}$ vetülete $E_{1} E_{2}$ -re $Q,$ és $O_{2}$ vetülete $Q O_{3}$ -ra $R,$ $E_{1} E_{4} = x$ és $E_{2} E_{3} = y .$

r_{2} ≦ r_{3}

választása mellett a körök háromféleképpen helyezkedhetnek el, aszerint, hogy

r_{3} > r_{1}, r_{3} < r_{1}

, ill.

r_{3} = r_{1}

. Mindhárom esetben létrejönnek az

O_{1} P O_{2}, O_{1} Q O_{3}, O_{2} R O_{3}

(esetleg elfajuló) derékszögű háromszögek.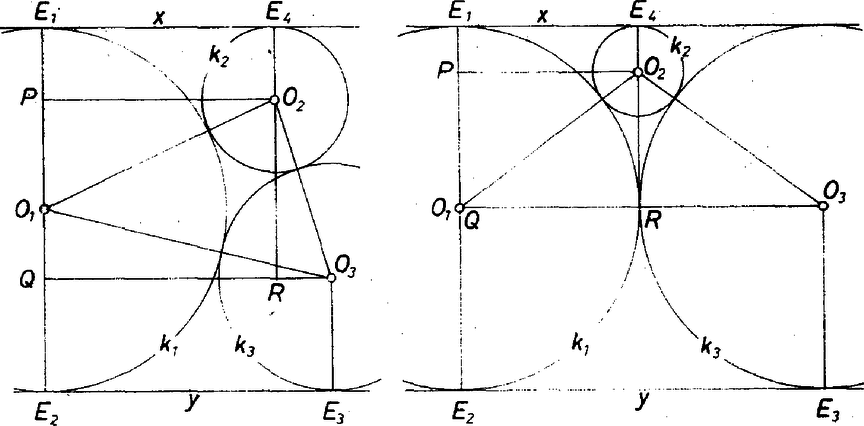

Felhasználva, hogy egymást kívülről érintő körök középpontjait összekötő egyenes áthalad a közös érintési ponton, és a középpontok távolsága a körök sugarának összege, e három háromszögre felírhatjuk Pitagorasz tételét:

\begin{matrix} {(r_{1} + r_{2})}^{2} = x^{2} + {(r_{1} - r_{2})}^{2}, & (1) \\ {(r_{1} + r_{3})}^{2} = y^{2} + {(r_{1} - r_{3})}^{2}, & (2) \\ {(r_{2} + r_{3})}^{2} = {(y - x)}^{2} + {(2 r_{1} - r_{2} - r_{3})}^{2}, & (3) \end{matrix}

Az (1) összefüggésből

x = 2 \sqrt[]{r_{1} r_{2}},

(2)-ből

y = 2 \sqrt[]{r_{1} r_{3}}

. Ezeket (3)-ba helyettesítve

\begin{matrix} {(r_{2} + r_{3})}^{2} = {(2 \sqrt[]{r_{1} r_{3}} - 2 \sqrt[]{r_{1} r_{2}})}^{2} + 4 r_{1}^{2} - 4 r_{1} (r_{2} + r_{3}) + {(r_{2} + r_{3})}^{2}, \end{matrix}

ahonnan

4 r_{2} r_{3} = r_{1}^{2} .

Ezt akartuk bizonyítani.

Bangha Imre (Győr, Czuczor G. Bencés Gimn., II. o. t.)
dolgozata alapján