Kezdőlap


Feladat:	Gy.2110	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1983/október, 68 - 69. oldal		PDF \| MathML
Témakör(ök):	Sakktáblával kapcsolatos feladatok, Gyakorlat, Kombinatorikai leszámolási problémák
Hivatkozás(ok):	Feladatok: 1983/március: Gy.2110

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Nyilván feltehetjük, hogy $k \leq n$ . Ha a bábukat a kívánt módon helyezzük el, akkor minden bástyához egyértelműen rendelhető hozzá az általa ütött bástya. Így bizonyos, hogy a kívánt módon csak páros számú bástyát lehet elhelyezni. Nevezzünk két egymást ütő bástyát "pár''-nak, a sakktábla sorait és oszlopait együttesen sávoknak. Egy pár 3 sávot foglal le, erre a 3 sávra további bástyát nem helyezhetünk.

k \times n

-es sakktáblán

k + n

sáv áll rendelkezésre, így legfeljebb

[\frac{k + n}{3}]

pár‐ azaz

2 \cdot [\frac{k + n}{3}]

bástya ‐ helyezhető el a kívánt módon.
Ugyanakkor a párok száma nyilván nem lehet nagyobb sem a vízszintes, sem pedig a függőleges sávok számánál. Ez

k \leq n

miatt a

2 k

felső becslést adja.
Ha

n > 2 k

, akkor ez utóbbi becslés kisebb az előbbinél, másrészt ilyenkor

2 k

bástya el is helyezhető a kívánt módon (1. ábra).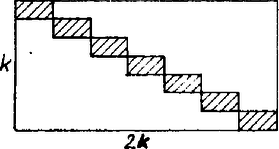

1. ábra

n \leq 2 k

, akkor

2 \cdot [\frac{k + n}{3}] \leq 2 k

. Megmutatjuk, hogy

k \leq n \leq 2 k

esetén a

k \times n

-es sakktáblán

[\frac{k + n}{3}]

megfelelő pár helyezhető el.
Láttuk, hogy azok a sakktáblák, amelyeknek egyik oldala kétszer akkora, mint a másik, kitölthetők a hosszabb oldalukkal párhuzamos állású párokkal. Próbáljuk ilyen részekre osztani a sakktáblánkat: (2. ábra)

2. ábra

Az ábra jelölései szerint:

x + 2 y = n

y + 2 x = k

, ahonnan

\begin{matrix} x = \frac{2 k - n}{3} és y = \frac{2 n - k}{3} . \end{matrix}

Ha ezek a számok egészek, akkor vízszintesen és függőlegesen összesen

x + y =

= \frac{k + n}{3}

pár helyezhető el, ez pedig éppen

[\frac{k + n}{3}]

, hisz az egészrész jelen belül most egész szám áll.
Ha

x

vagy

y

nem egész, akkor a vízszintes téglalap oldalait

[x]

-nek és

2 [x]

-nek választjuk. A függőleges téglalap oldalai most

k - 2 [x]

és

n - [x]

, ebben kell elhelyeznünk a hiányzó

u = [\frac{k + n}{3}] - [x]

párt. Ez biztosan megtehető, ha a függőleges téglalap tartalmaz

u \times 2 u

oldalú résztéglalapot, azaz ha

\begin{matrix} k - 2 [x] \geq u és n - [x] \geq 2 u . \end{matrix}

Az első egyenlőtlenség behelyettesítés és rendezés után a

\begin{matrix} [\frac{k + n}{3}] + [\frac{2 k - n}{3}] \leq k \end{matrix}

alakot ölti. Ez pedig teljesül, hiszen az egészrész-jeleken belül levő számok összege

k

. A második egyenlőtlenségből, mivel

n

egész, és így

n + [x] = [n + x]

\begin{matrix} 2 \cdot [\frac{k + n}{3}] \leq n + [\frac{2 k - n}{3}] = [2 \cdot \frac{k + n}{3}] \end{matrix}

adódik. A

2 [t] \leq [2 t]

egyenlőtlenség viszont minden számra teljesül.

Összefoglalva tehát: ha

n > 2 k

, akkor a

k \times n

-es sakktáblán legfeljebb

2 k

, ha pedig

k \leq n \leq 2 k

, akkor

2 \cdot [\frac{k + n}{3}]

darab bástya állítható föl a kívánt módon.

Megjegyzés. Sokan igazolták, hogy

2 k

, ill.

2 \cdot [\frac{k + n}{3}]

felső korlátok ‐ ez lényegében a 2064. gyakorlat megoldásából is kiderül ‐, azt azonban már nem vizsgálták, hogy ezek a korlátok elérhetők-e.