Kezdőlap


Feladat:	Gy.2108	Korcsoport: 16-17	Nehézségi fok: nehéz
Füzet:	1983/október, 67 - 68. oldal		PDF \| MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Ceva-tétel, Középvonal, Súlyvonal, Szögfelező egyenes, Gyakorlat
Hivatkozás(ok):	Feladatok: 1983/február: Gy.2108

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük $B C$ felezőpontját $F$ -fel, a $C$ -ből induló magasság talppontját $P$ -vel, $P B$ felezőpontját $Q$ -val. Ekkor persze $F Q$ középvonala a $C P B$ háromszögnek.

B

-ből induló belső szögfelező szögfelezője az

A F B

háromszögnek 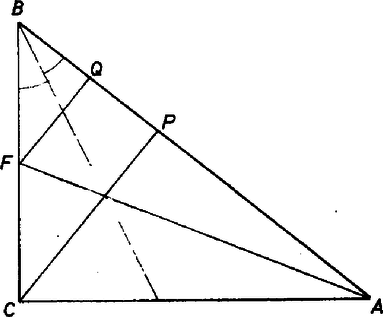is, tehát ez az egyenes az

A F

szakaszt a közrezáró oldalak arányában osztja:

\begin{matrix} A B : B F = A B : \frac{B C}{2} = \frac{2 A B}{B C} . \end{matrix}

(1)

Azt, hogy a

C P

magasságvonal az AF szakaszt milyen arányban osztja, a párhuzamos szelők tétele alapján számíthatjuk ki. Mivel

C P ∥ F Q

, ez az arány

\begin{matrix} A P : P Q = A P : \frac{P B}{2} = \frac{A P}{P C} : \frac{P B}{2 P C} = \frac{A C}{C B} : \frac{C B}{2 A C} = 2 \cdot \frac{A C^{2}}{B C^{2}} . & (2) \end{matrix}

Itt kihasználtuk, hogy az

A P C

C P B

, valamint

A C B

háromszögek hasonlóak.
A kérdezett három egyenes akkor és csak akkor megy át egy ponton, ha a szögfelező és a magasságvonal ugyanolyan arányban osztja a súlyvonalat, azaz ha az (1) és (2) alatti arányok egyenlők:

\begin{matrix} \frac{2 A B}{B C} = \frac{2 A C^{2}}{B C^{2}}, \end{matrix}

vagyis ha

A B \cdot B C = A C^{2}

. Ezzel a feladat állítását beláttuk.

Megjegyzések. 1. A feladat állítása könnyen adódik Ceva tételéből: Az

A B C

háromszög

B C

C A

A B

oldalszakaszain felvéve az

A_{1}

B_{1}

C_{1}

pontokat,

A A_{1}

B B_{1}

C C_{1}

akkor és csak akkor megy át egy ponton, ha

\begin{matrix} \frac{B A_{1}}{A_{1} C} \cdot \frac{C B_{1}}{B_{1} A} \cdot \frac{A C_{1}}{C_{1} B} = 1. \end{matrix}

Ennek alapján a feladat könnyen általánosítható tetszőleges háromszögre.
2. Egy

A B

átfogójú derékszögű háromszög oldalaira akkor és csak akkor teljesül az

A C^{2} = B C \cdot A B

összefüggés, ha a háromszög oldalainak aránya

\begin{matrix} A B : B C : C A = (1 + \sqrt[]{5}) : 2 : \sqrt[]{2 + 2 \sqrt[]{5}} . \end{matrix}